Точка делит вектор в отношении

Когда существуют условия деления отрезка в определенном отношении, необходимо уметь определять координаты точки, служащей разделителем. Выведем формулу для нахождения этих координат, поставив задачу на плоскости.

Определение координат точки, делящей отрезок в заданном отношении, на плоскости

Исходные данные: задана прямоугольная система координат O x y и две лежащие на ней, несовпадающие точки с заданными координатами A ( x A , y A ) и B ( x B , y B ) . А также задана точка С , делящая отрезок А В в отношении λ (некоторое положительное действительное число). Необходимо определить координаты точки С : x C и y C .

Перед тем, как приступить к решению поставленной задачи, немного раскроем смысл заданного условия: «точка С , делящая отрезок А В в отношении λ ». Во-первых, это выражение свидетельствует о том, что точка С лежит на отрезке А В (т.е. между точками А и В ). Во-вторых, понятно, что согласно заданному условию отношение длин отрезков А С и С В равно λ . Т.е. верно равенство:

В этом случае точка А – начало отрезка, точка В – конец отрезка. Если бы было задано, что точка С делит в заданном отношении отрезок В А , тогда верным было бы равенство: .

Ну и совсем очевидный факт, что если λ = 1 , то точка С является серединой отрезка А В .

Решим поставленную задачу при помощи векторов. Отобразим произвольно в некой прямоугольной системе координат точки А , В и точку С на отрезке А В . Построим радиус-векторы указанных точек, а также векторы A C → и C B → . Согласно условиям задачи, точка С делит отрезок А В в отношении λ .

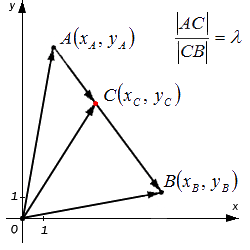
Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = ( x A , y A ) и O B → = ( x B , y B ) .

Определим координаты вектора : они будут равны координатам точки С , которые и требуется найти по условию задачи.

Используя операцию сложения векторов, запишем равенства: O C → = O A → + A C → O B → = O C → + C B → ⇔ C B → = O B → — O C →

По условию задачи точка С делит отрезок А В в отношении λ , т.е. верно равенство A C = λ · C B .

Векторы A C → и C B → лежат на одной прямой и являются сонаправленными. λ > 0 по условию задачи, тогда, согласно операции умножения вектора на число, получим: A C → = λ · C B → .

Преобразуем выражение, подставив в него : C B → = O B → — O C → .

A C → = λ · ( O B → — O C → ) .

Равенство O C → = O A → + A C → перепишем как O C → = O A → + λ · ( O B → — O C → ) .

Используя свойства операций над векторами, из последнего равенства следует: O C → = 1 1 + λ · ( O A → + λ · O B → ) .

Теперь нам остается непосредственно вычислить координаты вектора O C → = 1 1 + λ · O A → + λ · O B → .

Выполним необходимые действия над векторами O A → и O B → .

O A → = ( x A , y A ) и O B → = ( x B , y B ) , тогда O A → + λ · O B → = ( x A + λ · x B , y A + λ · y B ) .

Таким образом, O C → = 1 1 + λ · ( O A → + λ · O B → ) = ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ ) .

Резюмируя: координаты точки С , делящей отрезок А В в заданном отношении λ определяются по формулам : x C = x A + λ · x B 1 + λ и y C = у A + λ · y B 1 + λ .

Определение координат точки, делящей отрезок в заданном отношении, в пространстве

Исходные данные: прямоугольная система координат O x y z , точки с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) .

Точка С делит отрезок А В в отношении λ . Необходимо определить координаты точки С .

Используем ту же схему рассуждений, что и в случае выше на плоскости, придем к равенству:

O C → = 1 1 + λ · ( O A → + λ · O B → )

Векторы и являются радиус-векторами точек А и В , а значит:

O A → = ( x A , y A , z A ) и O B → = ( x B , y B , z B ) , следовательно

O C → = 1 1 + λ · ( O A → + λ · O B → ) = ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ , z A + λ · z B 1 + λ )

Таким образом, точка С , делящая отрезок А В в пространстве в заданном отношении λ , имеет координаты: ( x A + λ · x B 1 + λ , y A + λ · y B 1 + λ , z A + λ · z B 1 + λ )

Рассмотрим теорию на конкретных примерах.

Исходные данные: точка С делит отрезок А В в отношении пять к трем. Координаты точек А и В заданы A ( 11 , 1 , 0 ) , B ( — 9 , 2 , — 4 ) .

Решение

По условию задачи λ = 5 3 . Применим полученные выше формулы и получим:

x A + λ · x B 1 + λ = 11 + 5 3 · ( — 9 ) 1 + 5 3 = — 3 2

y A + λ · y B 1 + λ = 1 + 5 3 · 2 1 + 5 3 = 13 8

z A + λ · z B 1 + λ = 0 + 5 3 · ( — 4 ) 1 + 5 3 = — 5 2

Ответ: C ( — 3 2 , 13 8 , — 5 2 )

Исходные данные: необходимо определить координаты центра тяжести треугольника А В С .

Заданы координаты его вершин: A ( 2 , 3 , 1 ) , B ( 4 , 1 , — 2 ) , C ( — 5 , — 4 , 8 )

Решение

Известно, что центром тяжести любого треугольника является точка пересечения его медиан (пусть это будет точка М ). Каждая из медиан делится точкой М в отношении 2 к 1 , считая от вершины. Исходя из этого, найдем ответ на поставленный вопрос.

Допустим, что А D – медиана треугольника А В С . Точка М – точка пересечения медиан, имеет координаты M ( x M , y M , z M ) и является центром тяжести треугольника. М , как точка пересечения медиан, делит отрезок А D в отношении 2 к 1 , т.е. λ = 2 .

Найдем координаты точки D . Так как A D – медиана, то точка D – середина отрезка В С . Тогда, используя формулу нахождения координат середины отрезка, получим:

x D = x B + x C 2 = 4 + ( — 5 ) 2 = — 1 2 y D = y B + y C 2 = 1 + ( — 4 ) 2 = — 3 2 z D = z B + z C 2 = — 2 + 8 2 = 3

Вычислим координаты точки М :

x M = x A + λ · x D 1 + λ = 2 + 2 · ( — 1 2 ) 1 + 2 = 1 3

y M = y A + λ · y D 1 + λ = 3 + 2 · ( — 3 2 ) 1 + 2 = 0

z M = z A + λ · z D 1 + λ = 1 + 2 · 3 1 + 2 = 7 3

§1. Система координат

1.1 Система координат на плоскости (пространство r2 )

Декартовая прямоугольная система координат на плоскости считается заданной, если заданы две взаимно перпендикулярные прямые (оси координат), начало отcчёта и единица масштаба.

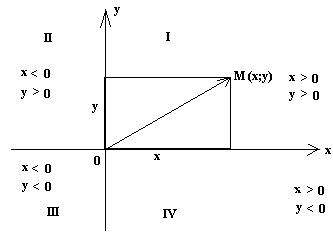рис.1

Горизонтальная ось — ось абсцисс, положительное направление оси — вправо.

Вертикальная ось, перпендикулярная к первой, называется осью ординат. Положительное направление — вверх.

Положение точки на плоскости определяется двумя числами — абсциссой и ординатой. Они называются координатами точки.

Координаты пишутся в круглых скобках рядом с названием точки, причем на первом месте в прямоугольной системе координат записывается абсцисса точки, а на втором — ее ордината. Например, если x-абсцисса точки, а y — ее ордината, то это записывается так: A(x;y). У точек, лежащих на оси абсцисс, ординаты равны нулю, а у точек, лежащих на оси ординат — абсциссы равны нулю. Абсцисса и ордината точки есть расстояния этой точки до осей ОY и ОХ соответственно, которым приписываются определённые знаки в зависимости от четверти, на которые оси координат делят всю координатную плоскость.

Четверти (квадранты) и знаки координат указаны на рисунке 1. Если соединить точку с началом координат, получим вектор , который называется радиусом — вектором точки М. Координаты радиуса — вектора совпадают с координатами точки.

1.2 Простейшие задачи аналитической геометрии Расстояние между двумя точками на плоскости

Пусть заданы две точки А(х₁;y₁) и B(x₂;y₂). Требуется найти расстояние АВ между ними.

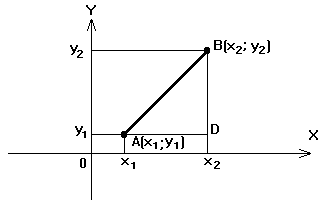Рис. 2

АВ=. (1.1)

Расстояние между двумя точками на плоскости равно корню квадратному из суммы квадратов разностей одноимённых координат.

Слагаемые в круглых скобках можно менять местами, т.к. каждая скобка возводится в квадрат.

Деление отрезка в данном отношении

Пусть А(х₁;у₁) и В(х₂;у₂) концы отрезка АВ. Точка С(х;у) делит отрезок АВ в отношении .

Требуется найти координаты точки С (рисунок 3).

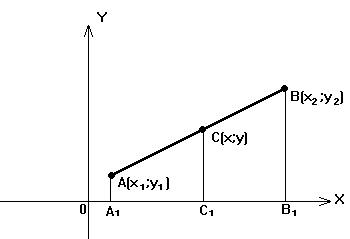Рис. 3

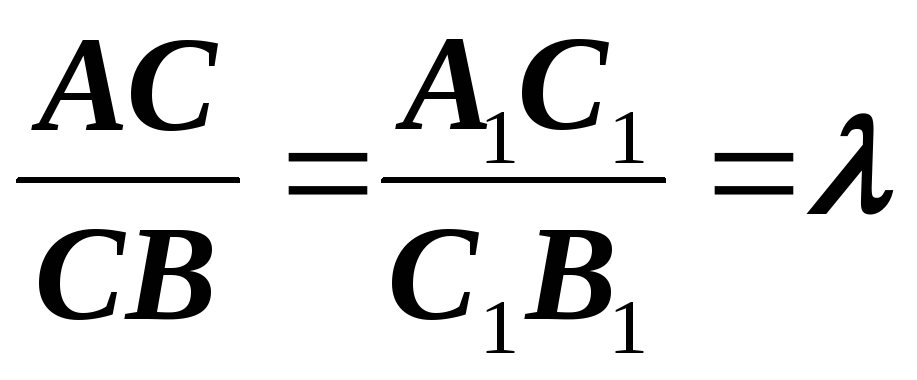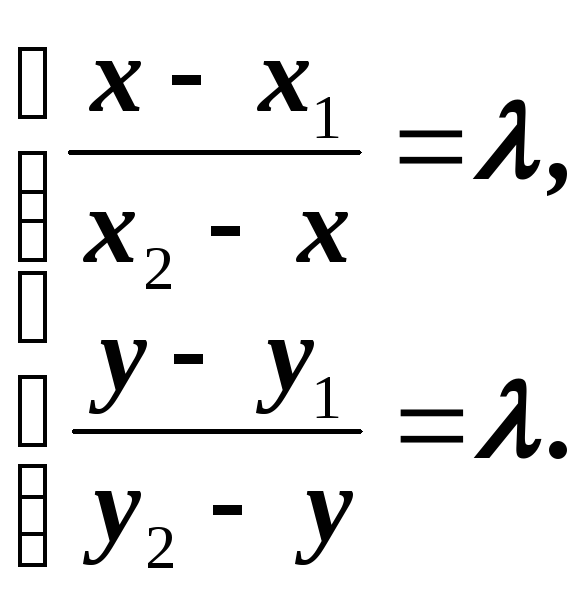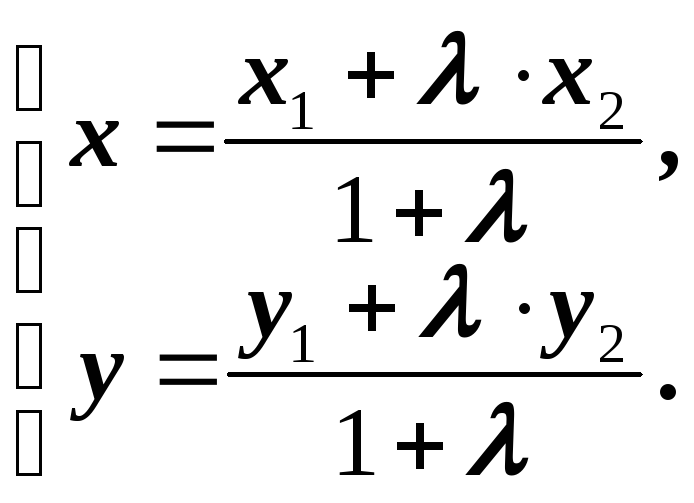Так как  ( на основе теоремы о пересечении отрезка параллельными прямыми) (1.2)(1.3)

Если разрешить уравнения (1.2) относительно Х и У получатся формулы (1.3). Если =1, то есть точкаС-середина АВ, и

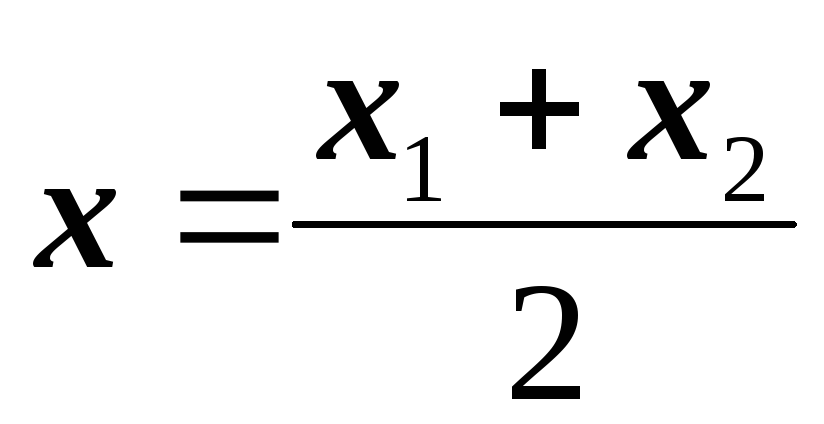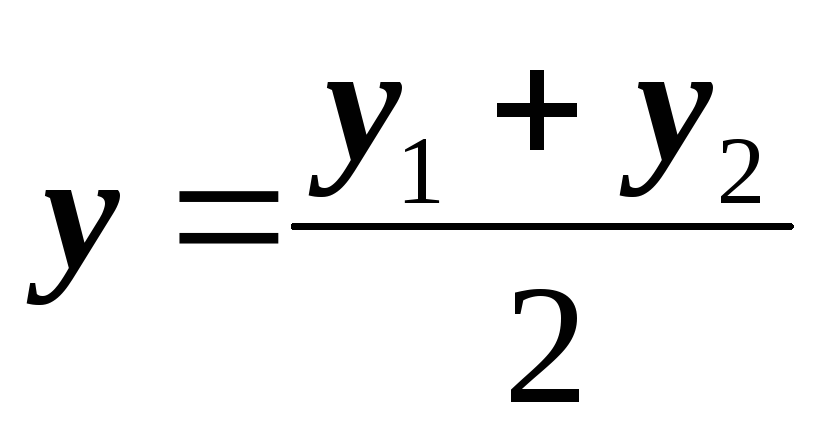; (1.4)

Замечание. Если точка С вне отрезка АВ — за концом отрезка, то — отрицательное число (рисунок 4).

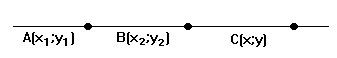Рис. 4

, т.к. направление отрезков АС и СВ — противоположны .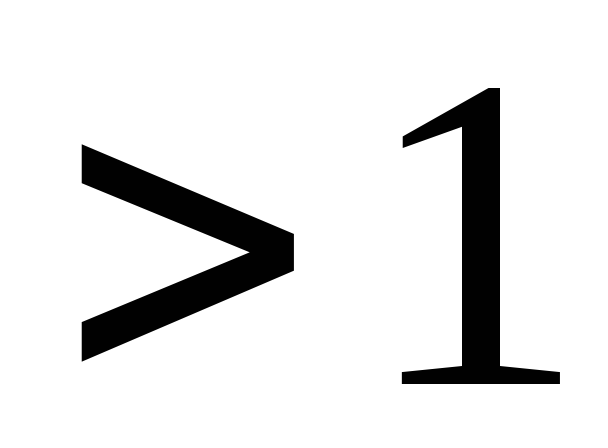

б) С — за началом отрезка (рисунок 5).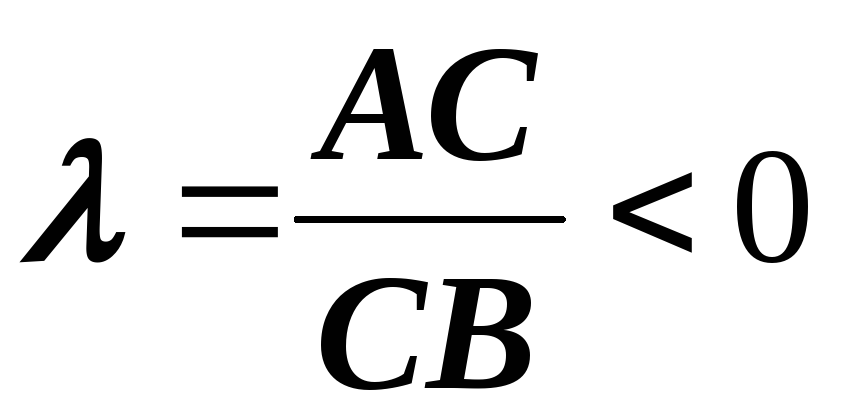и.

Рис. 5

§2 Векторы.

Линейные операции с векторами

Проекция вектора на ось

Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы.

Действия над векторами в координатной форме.

1.Основные понятия

Опр.1 Величины, которые полностью определяются своими

численными значениями, называются скалярными.

Опр. 2 Вектором называется направленный прямолинейный отрезок.

Обозначается или . Вектор считается заданным, если известны его длина и направление.

Опр.3 Число, равное длине вектора, называется его модулем или длиной вектора.

Обозначается или . Модуль может быть только положительным числом.

Векторы в пространстве свободны, т.е. начало его (точку приложения) можно поместить в любую точку пространства, при этом нужно сохранить длину и направление.

Опр.4 Вектор ВА называется противоположным Вектору АВ.

Опр 5 Вектор называется единичным (е), если длина его равна 1, а если его направление совпадает с направлением данного вектора, то он называется ортом вектора а.

Опр 6 Вектор называется нулевым, если совпадают координаты его

начальной и конечной точек.

Длина нулевого вектора равна нулю.

Опр 7 Векторы иназываютсяколлинеарными, если они лежат

на одной прямой или на параллельных прямых. .

Направления их могут быть одинаковыми или противоположными.

Опр. 8 Векторы иназываютсяравными, если они коллинеарные,

имеют одинаковую длину и направление().

Опр. 9 Векторы, лежащие в одной плоскости, называются

Nav view search

Navigation

Search

• Вы здесь:
• Home
• Высшая математика.
• Аналитическая геометрия.
• Деление отрезка в заданном отношении (векторный и координатный способы).

Деление отрезка в заданном отношении (векторный и координатный способы).

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Зная координаты точек $M_1(x_1, y_1, z_1)$ и $M_2(x_2, y_2, z_2)$ и отношение $lambda,$ в котором точка $M$ делит направленный отрезок $overline,$ найдем координаты точки $M.$

Пусть $O -$ начало координат. Обозначим $overline=r_1,$ $overline=r_2,$ $overline=r.$ Так как, $$overline=r-r_1, overline=r_2-r,$$ то $r-r_1=lambda(r_2-r),$ откуда (так как $lambda
eq -1$) $$r=frac<1+lambda>.$$ Полученная форма и дает решение задачи в векторной форме. Переходя в этой формуле к координатам, получим $$x=frac<1+lambda>, y=frac<1+lambda>, z=frac<1+lambda>.$$

Примеры.

2.57. Отрезок с концами в точках $A(3, -2)$ и $B(6, 4)$ разделен на три равные части. Найти координаты точек деления.

Решение.

Пусть $C(x_C, y_C)$ и $D(x_D, y_D) -$ точки, которые делят отрезок $AB$ на три равные части. Тогда $$lambda_1=frac=frac<1><2>;$$ $$x_C=frac<1+lambda_1>=frac<3+frac<1><2>cdot 6><1+frac<1><2>>=4;$$

Далее находим координаты точки $D:$

Ответ: $(4, 0)$ и $(5, 2).$

2.58. Определить координаты концов отрезка, который точками $C(2, 0, 2)$ и $D(5, -2, 0)$ разделен на три равные части.

Решение.

Пусть $A(x_A, y_A, z_A)$ и $B(x_B, y_B, z_B) -$ концы заданного отрезка.

Выпишем формулы для нахождения координат точки $C$ и подставим известные координаты:

Аналогичные равенства запишем для точки $D:$

Далее запишем полученные уравнения относительно $x_A, x_B;$ $y_A, y_B$ и $z_A, z_B$ попарно в виде систем и решим их:

Таким образом, получили координаты концов отрезка $A(-1, 2, 4)$ и $B(8, -4, -2).$

Ответ: $A(-1, 2, 4),$ $B(8, -4, -2).$