СТЕПЕНЬ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ,
СТЕПЕННАЯ ФУНКЦИЯ IV
§ 70. Сравнение степеней
Теорема 1. Из двух степеней с одинаковыми показателями и положительными основаниями больше та, основание которой больше. Другими словами, если а > b > 0, то при любом натуральном п
Это свойство было доказано нами в главе I (§ 12).
Пример. Какое число больше: 2 300 или 3 200 ?
Для решения этой задачи представим данные числа в виде степеней с одинаковыми показателями, используя тождество
2 300 = 2 3•100 = (2 3 ) 100 =8 100 3 200 = 3 2•100 = (3 2 ) 100 = 9 100
Так как 9 > 8, то 9 100 > 8 100 . Следовательно,
Теорема 2. Если 0 m и а n больше та, показатель которой меньше.
Если а >1, то из двух степеней а m и а n больше та, показатель которой больше.
Доказательство. Пусть m > п. Тогда т = п + k, где k — некоторое натуральное число. Поэтому
Например, ( 1 /3 ) 100 1 /3 ) 50 ; 3 100 > 3 50
526. Данные выражения представить в виде степеней с одинаковыми показателями и сравнить их по величине:
1) 4 2 и 2 8 ; 4) 4 300 и 3 400 ; 6) ( — 6 /7 ) 4 и ( 36 /49) 6 ;
2) 27 3 и 9 6 ; 5) — 1 /8 и (— 1 /32) 3 ; 7) ( 1 /16) 100 и ( 1 /2) 500 .
527. Данные выражения представить в виде степеней с одинаковыми основаниями и сравнить их по величине:
1) 8 5 и 16 3 ; 3) (—3) 75 и (—27) 15 ;
2) 4 100 и 32 50 ; 4) 81 150 • 8 200 и 3 600 • 16 75 .
 Свойства степеней с рациональными показателями Свойства степеней с рациональными показателями |
 Понятие о степени с иррациональным показателем Понятие о степени с иррациональным показателем |

Пусть p – произвольное положительное рациональное число. Тогда это рациональное число можно представить в виде несократимой дроби
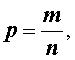
где m и n – натуральные числа. Предположим также, что a – произвольное положительное действительное число.
Теперь мы можем дать определение степени с рациональным показателем .
Определение . Степень, показатель которой есть положительное рациональное число , определяется по формуле:
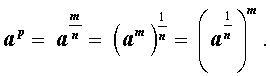
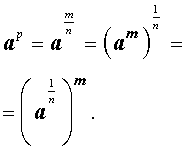
Определение . Степень, показатель которой есть отрицательное рациональное число , определяется по формуле:
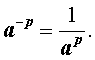
Определение . Степень с нулевым показателем определяется по формуле:
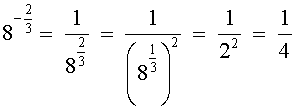
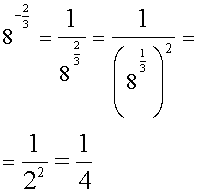
Свойства степеней с рациональными показателями
Для степеней с рациональными показателями выполняются следующие свойства :
 |
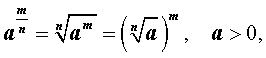
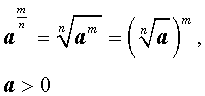

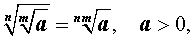

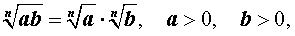
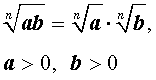

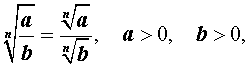
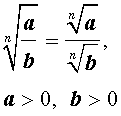
Кроме того, если p и q – произвольные рациональные числа, то

a > 0 ,

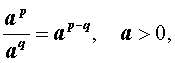


a > 0 , b > 0 ,

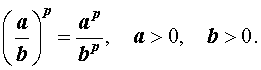
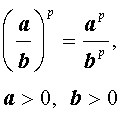
Замечание . Желающие могут ознакомиться с нашей презентацией «Степень с рациональным показателем», содержание которой связано с данным разделом.
Понятие о степени с иррациональным показателем
Кроме степеней с рациональными показателями в математике и других точных науках большое значение имеют и степени с иррациональными показателями , однако их определение выходит за рамки курса средней школы. Упомянем лишь о том, что степень с иррациональным показателем строится с помощью предельного перехода по последовательностям степеней с рациональными показателями, которые являются приближениями иррационального показателя степени с недостатком и с избытком.
С понятиями степени с целочисленным показателем и арифметического корня можно ознакомиться в разделе «Степень с целочисленным показателем и арифметический корень» нашего справочника.
Графики степенных и показательных функций представлены в разделе «Графики степенных, показательных и логарифмических функций» нашего справочника.
Как сравнивать степени с одинаковыми основаниями? С одинаковыми показателями? Можно ли сравнить степени, если и основания, и показатели различны?
Как и сравнение логарифмов, сравнение степеней основано на свойстве показательной функции.
Сравнение степеней с одинаковыми основаниями
- Если основание степени больше единицы (a>1), показательная функция возрастает, большему значению аргумента соответствует большее значение функции, соответственно, знак неравенства между показателями степеней и между степенями одинаковый.
- Если основание степени меньше единицы (0
С помощью схемы сравнение степеней с равными основаниями можно изобразить так:

№1. Сравнить значения выражений:
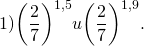
Сравниваем показатели степеней: 1,5 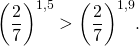 <left( <frac<2><7>>
<left( <frac<2><7>>
ight)^<1,9>>.]" title="Rendered by QuickLaTeX.com"/>
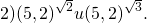
Сравниваем показатели степеней:
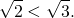
Основание a=5,2 больше единицы, функция возрастает, знак неравенства между степенями не меняется:
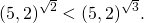
№2. Сравнить показатели m и n, если известно, что для степеней выполняется неравенство:
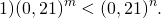
Основание a=0,21 n.
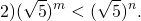
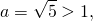 1,]" title="Rendered by QuickLaTeX.com"/>
1,]" title="Rendered by QuickLaTeX.com"/>
функция возрастает, поэтому знак неравенства между показателями степеней не изменяется: m Сравнение степеней с одинаковыми показателями .
1) Для возрастающих функций ( x>0):
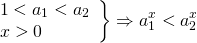 0 end
0 end
ight> Rightarrow a_1^x
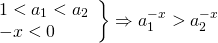 a_2^< — x>]" title="Rendered by QuickLaTeX.com"/>
a_2^< — x>]" title="Rendered by QuickLaTeX.com"/>
Для положительных значений аргумента
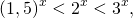
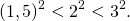
Для отрицательных значений аргумента
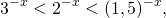
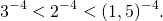

2) Для убывающих функций:
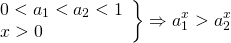 0 end
0 end
ight> Rightarrow a_1^x > a_2^x]" title="Rendered by QuickLaTeX.com"/>
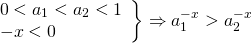 a_2^< — x>]" title="Rendered by QuickLaTeX.com"/>
a_2^< — x>]" title="Rendered by QuickLaTeX.com"/>
Для положительных значений аргумента
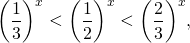
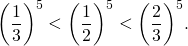
Для отрицательных значений аргумента:
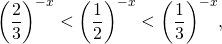
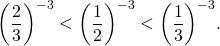

Как сравнивать степени, если и основания, и показатели различны?
Можно попробовать, например, сравнить каждую из степеней с единицей. Любая степень с основанием, большим единицы, при положительных значениях аргумента принимает значения, большие единицы:
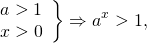 1\ x > 0 end
1\ x > 0 end
ight> Rightarrow > 1,]" title="Rendered by QuickLaTeX.com"/>
при отрицательных — меньшие 1:
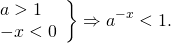 1\ — x
1\ — x
Если основание меньше единицы — соответственно,
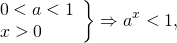 0 end
0 end
ight> Rightarrow
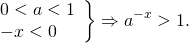 1.]" title="Rendered by QuickLaTeX.com"/>
1.]" title="Rendered by QuickLaTeX.com"/>
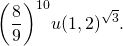
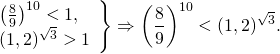 1 end
1 end
ight> Rightarrow <left( <frac<8><9>>
ight)^<10>>
В алгебре сравнивать степени чаще всего приходится при решении показательных неравенств.
Как решать показательные неравенства, мы рассмотрим позже.