Разряды чисел после запятой

В названиях арабских чисел каждая цифра принадлежит своему разряду, а каждые три цифры образуют класс. Таким образом, последняя цифра в числе обозначает количество единиц в нем и называется, соответственно, разрядом единиц. Следующая, вторая с конца, цифра обозначает десятки (разряд десятков), и третья с конца цифра указывает на количество сотен в числе – разряд сотен. Дальше разряды точно также по очереди повторяются в каждом классе, обозначая уже единицы, десятки и сотни в классах тысяч, миллионов и так далее. Если число небольшое и в нем нет цифры десятков или сотен, принято принимать их за ноль. Классы группируют цифры в числах по три, нередко в вычислительных приборах или записях между классами ставится точка или пробел, чтобы визуально разделить их. Это сделано для упрощения чтения больших чисел. Каждый класс имеет свое название: первые три цифры – это класс единиц, далее идет класс тысяч, затем миллионов, миллиардов (или биллионов) и так далее.

Поскольку мы пользуемся десятичной системой исчисления, то основная единица измерения количества – это десяток, или 10 1 . Соответственно с увеличением количества цифр в числе, увеличивается и количество десятков 10 2 , 10 3 , 10 4 и т.д. Зная количество десятков можно легко определить класс и разряд числа, например, 10 16 – это десятки квадриллионов, а 3×10 16 – это три десятка квадриллионов. Разложение чисел на десятичные компоненты происходит следующий образом – каждая цифра выводится в отдельное слагаемое, умножаясь на требуемый коэффициент 10 n , где n – положение цифры по счет слева направо.
Например: 253 981=2×10 6 +5×10 5 +3×10 4 +9×10 3 +8×10 2 +1×10 1

Также степень числа 10 используется и в написании десятичных дробей: 10 (-1) – это 0,1 или одна десятая. Аналогичным образом с предыдущим пунктом, можно разложить и десятичное число, n в таком случае будет обозначать положение цифры от запятой справа налево, например: 0,347629= 3×10 (-1) +4×10 (-2) +7×10 (-3) +6×10 (-4) +2×10 (-5) +9×10 (-6)

Названия десятичных чисел. Десятичные числа читаются по последнему разряду цифр после запятой, например 0,325 – триста двадцать пять тысячных, где тысячные – это разряд последней цифры 5 .

Округление числа означает введение ограничения числа цифр (отдельных чисел), которые используются при учетной записи числа. Существуют определенные правила, которые помогают решить, в каких случаях числа должны быть округлены, и как они должны быть округлены. Этот раздел поможет Вам понять эти правила и корректно применять их.

Проводя вычисления, числа, которые Вы используете в своей работе, будут представляться в одной из следующих форм:

• Целые числа 1;32;512
• Десятичные дроби с целой частью 2,5;40,67;600,2
• Простые десятичные дроби 0,1;0,03;0,007
• Обыкновенные дроби

Для удобства простые дроби будут использоваться только при получении результатов вычислений в разделе «Алгебра» данного модуля. Обыкновенные дроби могут быть преобразованы в десятичные дроби, путем деления числа, находящегося выше черты (числитель), на число, находящееся ниже черты (знаменатель). Например, могут быть записаны, как 3 ¸ 4 = 0,75.

В данном материале десятичные знаки будут обозначаться запятой ‘ , ‘, например, 2,1 (в англоязычной литературе используется ‘ . ’). Тысячи будут отмечаться интервалом между цифрами, изображающими сотни и тысячи, например, 13 456 означает тринадцать тысяч четыреста пятьдесят шесть.

1.1 Значащие цифры

Число цифр, которые должны быть оставлены для выражения результата вычисления, зависит от типа (этапа) вычисления и от его необходимой точности. Одним из способов ее установления является принятие решения о числе значащих цифр, подлежащих сохранению. ‘0’ не является значащей цифрой, если только он не стоит между двумя другими числами, например, 103, или если он не является последним десятичным знаком, например, 2,10. (Оба эти числа являются примерами чисел с тремя значащими цифрами). Например, число 13 456 с точностью до двух значащих чисел может быть записано как 13 000 (отметим, что нули не являются здесь значащими цифрами). Этот способ записи является удобным для представления результата, однако он не указывает на размер ответа. Например, 13 000 и 2,1 могут оба представлять результат округления до двух значащих цифр. Число значащих цифр может, однако, быть показателем точности задания числа. Это является одним из основных факторов, определяющих сколько значащих цифр следует удерживать.

1.2 Как пользоваться округлением

Округление может быть осуществлено путем учета необходимого количества значащих цифр, как это обсуждалось в последнем параграфе, либо как резервирование десятичных разрядов. Число десятичных разрядов есть число десятичных знаков после запятой. Например, число 2,10 имеет два десятичных разряда (но три значащие цифры).

В обычной практике округление производится с повышением, если цифра, подлежащая округлению, больше, либо равна пяти. Например, числа 2,55, 2,56, 2,57, 2,58 and 2,59 запишутся как 2,6 при округлении до двух значащих цифр. (или одного десятичного разряда). Числа 2,50, 2,51, 2,52, 2,53 и 2,54 запишутся как 2,5 при округлении до двух значащих цифр (или одного десятичного разряда). Такая операция называется округлением с понижением, и обычно применяется, если цифры не превышают значение 5.

В табл. 1 показано, как используются значащие цифры, десятичные разряды при округлении.

Значащие цифры, десятичные разряды и округление

Рассчи­тан­ноезначение	Число значащих цифр			Число десятичных разрядов
	Четыре	Три	Два	Четыре	Три	Два
525,7910	525,8	526	530	525,7910	525,791	525,79
0,003417	0,003417	0,00342	0,0034	0,0034	0,003	0,00

1.3 Когда использовать округление

Существуют две принципиальных причины, почему следует округлять числа, а именно, чтобы

дать ответ, имеющий смысл,

показать точность измерения.

Для некоторых расчетов ответ приобретает смысл, только если результат соотносится с предварительно установленным уровнем значимости. Простым примером этого может служить случай, когда Вы хотите рассчитать число человек, которые могут сидеть вокруг стола в 345 см в окружности. Если каждому отвести по 75 см, то разделив 345 на 75, получится 4,6 человек! Очевидно, 0,6 человека не имеют никакого смысла в случае, когда необходимо знать, сколько человек могут сидеть вокруг стола. Если применить правила округления, приведенные в разделе 1.2, ответ получится равным 5. Но это пример «обычной практики», и не дает очень осмысленный ответ. Пятерым сидеть будет тесно; в этом случае 4 будет лучшим ответом.

Всегда следует думать, что означает ответ с практической точки зрения.

Точность числа может следовать из числа десятичных разрядов значащих цифр, данных в числе. Например, если длина футбольного поля определяется в 110 м, это означает, что это поле измерено с точностью до 10 м. Его действительная длина может иметь значение между 105 м и 114 м. Если же длина поля зарегистрирована как 108,54 м, это означает, что она измерена с точностью до одной сотой метра (сантиметра). Это представляет собой очень точное измерение. Число десятичных разрядов, удерживаемое в этом случае, определяется методом измерения. Очевидно, на имеет смысла принимать 108,54 м за длину футбольного поля, если измерение произведено с помощью мерной ленты, на которой метр является наименьшим делением. Больше смысла будет говорить о величине 109 м, т.е. округлить до одного метра.

1.4 Как определить число десятичных знаков

Существует несколько простых правил, применяемых при установлении, сколько десятичных разрядов или значащих цифр должно быть сохранено в числе. Эти правила таковы:

• Подумайте о смысле полученного ответа. (Как в примере с числом людей, которых можно усадить вокруг стола).
• Если число есть результат расчета, то в нем должно быть сохранено столько десятичных разрядов или значащих цифр, сколько их содержится в наименее точном числе, использованном при вычислении. Например,

2,1 x 3,45 x 1.3 = 9,4185 = 9,4 (округленно)

• Если число является результатом измерения, обратите внимание, как оно получено и какая точность может быть. (Как в примере с футбольным полем.)
• Рассмотрите, с какой точностью необходимо получить результат. (Например, Ответ может быть округлен до ближайшего десятка.)

Данный материал мы посвятим такой важной теме, как десятичные дроби. Сначала определимся с основными определениями, приведем примеры и остановимся на правилах десятичной записи, а также на том, что из себя представляют разряды десятичных дробей. Далее выделим основные виды: конечные и бесконечные, периодические и непериодические дроби. В финальной части мы покажем, как точки, соответствующие дробным числам, расположены на оси координат.

Что такое десятичная запись дробных чисел

Так называемая десятичная запись дробных чисел может быть использована как для натуральных, так и для дробных чисел. Она выглядит как набор из двух и более цифр, между которыми есть запятая.

Десятичная запятая нужна для того, чтобы отделять целую часть от дробной. Как правило, последняя цифра десятичной дроби не бывает нулем, за исключением случаев, когда десятичная запятая стоит сразу после первого же нуля.

Какие можно привести примеры дробных чисел в десятичной записи? Это может быть 34 , 21 , 0 , 35035044 , 0 , 0001 , 11 231 552 , 9 и др.

В некоторых учебниках можно встретить использование точки вместо запятой ( 5 . 67 , 6789 . 1011 и др.) Это вариант считается равнозначным, но он более характерен для англоязычных источников.

Определение десятичных дробей

Основываясь на указанном выше понятии десятичной записи, мы можем сформулировать следующее определение десятичных дробей:

Десятичные дроби представляют собой дробные числа в десятичной записи.

Для чего нам нужна запись дробей в такой форме? Она дает нам некоторые преимущества перед обыкновенными, например, более компактную запись, особенно в тех случаях, когда в знаменателе стоят 1000 , 100 , 10 и др. или смешанное число. Например, вместо 6 10 мы можем указать 0 , 6 , вместо 25 10000 – 0 , 0023 , вместо 512 3 100 – 512 , 03 .

О том, как правильно представить в десятичном виде обыкновенные дроби с десятками, сотнями, тысячами в знаменателе, будет рассказано в рамках отдельного материала.

Как правильно читать десятичные дроби

Существуют некоторые правила чтения записей десятичных дробей. Так, те десятичные дроби, которым соответствуют их правильные обыкновенные эквиваленты, читаются почти так же, но с добавлением слов «ноль десятых» в начале. Так, запись 0 , 14 , которой соответствует 14 100 , читается как «ноль целых четырнадцать сотых».

Если же десятичной дроби можно поставить в соответствие смешанное число, то она читается тем же образом, как и это число. Так, если у нас есть дробь 56 , 002 , которой соответствует 56 2 1000 , мы читаем такую запись как «пятьдесят шесть целых две тысячных».

Что такое разряды в десятичных дробях

Значение цифры в записи десятичной дроби зависит от того, на каком месте она расположена (так же, как и в случае с натуральными числами). Так, в десятичной дроби 0 , 7 семерка – это десятые доли, в 0 , 0007 – десятитысячные, а в дроби 70 000 , 345 она означает семь десятков тысяч целых единиц. Таким образом, в десятичных дробях тоже существует понятие разряда числа.

Названия разрядов, расположенных до запятой, аналогичны тем, что существуют в натуральных числах. Названия тех, что расположены после, наглядно представлены в таблице:

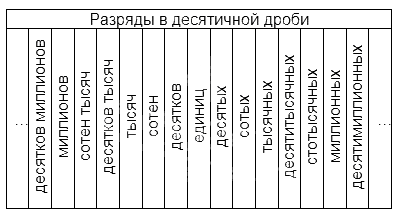
У нас есть десятичная дробь 43 , 098 . У нее в разряде десятков находится четверка, в разряде единиц тройка, в разряде десятых – ноль, сотых – 9 , тысячных – 8 .

Принято различать разряды десятичных дробей по старшинству. Если мы движемся по цифрам слева направо, то мы будем идти от старших разрядов к младшим. Получается, что сотни старше десятков, а миллионные доли младше, чем сотые. Если взять ту конечную десятичную дробь, которую мы приводили в качестве примера выше, то в ней старшим, или высшим будет разряд сотен, а младшим, или низшим – разряд 10 -тысячных.

Любую десятичную дробь можно разложить по отдельным разрядам, то есть представить в виде суммы. Это действие выполняется так же, как и для натуральных чисел.

Попробуем разложить дробь 56 , 0455 по разрядам.

У нас получится:

56 , 0455 = 50 + 6 + 0 , 4 + 0 , 005 + 0 , 0005

Если мы вспомним свойства сложения, то сможем представить эту дробь и в других видах, например, как сумму 56 + 0 , 0455 , или 56 , 0055 + 0 , 4 и др.

Что такое конечные десятичные дроби

Все дроби, о которых мы говорили выше, являются конечными десятичными дробями. Это означает, что количество цифр, расположенное у них после запятой, является конечным. Выведем определение:

Конечные десятичные дроби представляют собой вид десятичных дробей, у которых после знака запятой стоит конечное число знаков.

Примерами таких дробей могут быть 0 , 367 , 3 , 7 , 55 , 102567958 , 231 032 , 49 и др.

Любую из этих дробей можно перевести либо в смешанное число (если значение их дробной части отличается от нуля), либо в обыкновенную дробь (при нулевой целой части). Тому, как это делается, мы посвятили отдельный материал. Здесь просто укажем пару примеров: так, конечную десятичную дробь 5 , 63 мы можем привести к виду 5 63 100 , а 0 , 2 соответствует 2 10 (или любая другая равная ей дробь, например, 4 20 или 1 5 .)

Но обратный процесс, т.е. запись обыкновенной дроби в десятичном виде, может быть выполнен не всегда. Так, 5 13 нельзя заменить на равную дробь с знаменателем 100 , 10 и др., значит, конечная десятичная дробь из нее не получится.

Основные виды бесконечных десятичных дробей: периодические и непериодические дроби

Мы указывали выше, что конечные дроби называются так потому, что после запятой у них стоит конечное число цифр. Однако оно вполне может быть и бесконечным, и в этом случае сами дроби также будут называться бесконечными.

Бесконечными десятичными дробями называются такие, у которых после запятой стоит бесконечное количество цифр.

Очевидно, что полностью такие числа записаны быть просто не могут, поэтому мы указываем лишь часть из них и дальше ставим многоточие. Это знак говорит о бесконечном продолжении последовательности знаков после запятой. Примерами бесконечных десятичных дробей могут быть 0 , 143346732 … , 3 , 1415989032 … , 153 , 0245005 … , 2 , 66666666666 … , 69 , 748768152 … . и т.д.

В «хвосте» такой дроби могут стоять не только случайные на первый взгляд последовательности цифр, но постоянное повторение одного и того же знака или группы знаков. Дроби с чередованием после десятичной запятой называются периодическими.

Периодическими десятичными дробями называются такие бесконечные десятичные дроби, у которых после запятой повторяется одна цифра или группа из нескольких цифр. Повторяющаяся часть называется периодом дроби.

К примеру, для дроби 3 , 444444 … . периодом будет цифра 4 , а для 76 , 134134134134 … – группа 134 .

Какое же минимальное количество знаков допустимо оставить в записи периодической дроби? Для периодических дробей достаточно будет записать весь период один раз в круглых скобках. Так, дробь 3 , 444444 … . правильно будет записать как 3 , ( 4 ) , а 76 , 134134134134 … – как 76 , ( 134 ) .

В целом записи с несколькими периодами в скобках будут иметь точно такой же смысл: к примеру, периодическая дробь 0 , 677777 – это то же самое, что 0 , 6 ( 7 ) и 0 , 6 ( 77 ) и т.д. Также допустимы записи вида 0 , 67777 ( 7 ) , 0 , 67 ( 7777 ) и др.

Во избежание ошибок введем однообразие обозначений. Условимся записывать только один период (максимально короткую последовательность цифр), который стоит ближе всего к десятичной запятой, и заключать его в круглые скобки.

То есть для указанной выше дроби основной будем считать запись 0 , 6 ( 7 ) , а, например, в случае с дробью 8 , 9134343434 будем писать 8 , 91 ( 34 ) .

Если знаменатель обыкновенной дроби содержит простые множители, не равные 5 и 2 , то при переводе в десятичную запись из них получатся бесконечные дроби.

В принципе, любую конечную дробь мы можем записать в виде периодической. Для этого нам просто нужно добавить справа бесконечно много нулей. Как это выглядит в записи? Допустим, у нас есть конечная дробь 45 , 32 . В периодическом виде она будет выглядеть как 45 , 32 ( 0 ) . Это действие возможно потому, что добавление нулей справа в любую десятичную дробь дает нам в результате равную ей дробь.

Отдельно следует остановиться на периодических дробях с периодом 9 , например, 4 , 89 ( 9 ) , 31 , 6 ( 9 ) . Они являются альтернативной записью схожих дробей с периодом 0 , поэтому их часто заменяют при письме именно дробями с нулевым периодом. При этом к значению следующего разряда добавляют единицу, а в круглых скобках указывают ( 0 ) . Равенство получившихся чисел легко проверить, представив их в виде обыкновенных дробей.

К примеру, дробь 8 , 31 ( 9 ) можно заменить на соответствующую ей дробь 8 , 32 ( 0 ) . Или 4 , ( 9 ) = 5 , ( 0 ) = 5 .

Бесконечные десятичные периодические дроби относятся к рациональным числам. Иначе говоря, любую периодическую дробь можно представить в виде обыкновенной, и наоборот.

Существуют и дроби, у которых после запятой бесконечно повторяющаяся последовательность отсутствует. В таком случае их называют непериодическими дробями.

К непериодическим десятичным дробям относятся те бесконечные десятичные дроби, в которых после запятой не содержится периода, т.е. повторяющейся группы цифр.

Иногда непериодические дроби выглядят очень похожими на периодические. Например, 9 , 03003000300003 … на первый взгляд кажется имеющей период, однако подробный анализ знаков после запятой подтверждает, что это все же непериодическая дробь. С такими числами надо быть очень внимательным.

Непериодические дроби относятся к иррациональным числам. В обыкновенные дроби их не переводят.

Основные действия с десятичными дробями

С десятичными дробями можно производить следующие действия: сравнение, вычитание, сложение, деление и умножение. Разберем каждое из них отдельно.

Сравнение десятичных дробей может быть сведено к сравнению обыкновенных дробей, которые соответствуют исходным десятичным. Но бесконечные непериодические дроби свести к такому виду нельзя, а перевод десятичных дробей в обыкновенные зачастую является трудоемкой задачей. Как же быстро произвести действие сравнения, если нам нужно сделать это по ходу решения задачи? Удобно сравнивать десятичные дроби по разрядам таким же образом, как мы сравниваем натуральные числа. Этому методу мы посвятим отдельную статью.

Чтобы складывать одни десятичные дроби с другими, удобно использовать метод сложения столбиком, как для натуральных чисел. Чтобы складывать периодические десятичные дроби, необходимо предварительно заменить их обыкновенными и считать по стандартной схеме. Если же по условиям задачи нам надо сложить бесконечные непериодические дроби, то нужно перед этим округлить их до некоторого разряда, а потом уже складывать. Чем меньше разряд, до которого мы округляем, тем выше будет точность вычисления. Для вычитания, умножения и деления бесконечных дробей предварительное округление также необходимо.

Нахождение разности десятичных дробей обратно действию сложения. По сути, с помощью вычитания мы можем найти такое число, сумма которого с вычитаемой дробью даст нам уменьшаемую. Подробнее об этом расскажем в рамках отдельного материала.

Умножение десятичных дробей производится так же, как и для натуральных чисел. Для этого тоже подходит метод вычисления столбиком. Это действие с периодическими дробями мы опять же сводим к умножению обыкновенных дробей по уже изученным правилам. Бесконечные дроби, как мы помним, надо округлить перед подсчетами.

Процесс деления десятичных дробей является обратным процессу умножения. При решении задач мы также пользуемся подсчетами в столбик.

Положение десятичных дробей на оси координат

Можно установить точное соответствие между конечной десятичной дробью и точкой на оси координат. Выясним, как отметить точку на оси, которая будет точно соответствовать необходимой десятичной дроби.

Мы уже изучали, как построить точки, соответствующие обыкновенным дробям, а ведь десятичные дроби можно привести к такому виду. Например, обыкновенная дробь 14 10 – это то же самое, что и 1 , 4 , поэтому соответствующая ей точка будет удалена от начала отсчета в положительном направлении ровно на такое же расстояние:

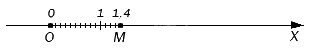
Можно обойтись без замены десятичной дроби на обыкновенную, а взять на основу метод разложения по разрядам. Так, если нам надо отметить точку, координата которой будет равна 15 , 4008 , то мы предварительно представим это число в виде суммы 15 + 0 , 4 + , 0008 . Для начала отложим от начала отсчета 15 целых единичных отрезков в положительном направлении, потом 4 десятых доли одного отрезка, а потом 8 десятитысячных долей одного отрезка. В итоге мы получим точку координат, которой соответствует дробь 15 , 4008 .

Для бесконечной десятичной дроби лучше пользоваться именно этим способом, поскольку он позволяет приблизиться к нужной точке сколь угодно близко. В некоторых случаях можно построить и точное соответствие бесконечной дроби на оси координат: так, 2 = 1 , 41421 . . . , и с этой дробью может быть соотнесена точка на координатном луче, удаленная от 0 на длину диагонали квадрата, сторона которого будет равна одному единичному отрезку.

Если мы находим не точку на оси, а десятичную дробь, соответствующую ей, то это действие называется десятичным измерением отрезка. Посмотрим, как правильно это сделать.

Допустим, нам нужно попасть от нуля в заданную точку на оси координат (или максимально приблизиться в случае с бесконечной дробью). Для этого мы постепенно откладываем единичные отрезки от начала координат, пока не попадем в нужную точку. После целых отрезков при необходимости отмеряем десятые, сотые и более мелкие доли, чтобы соответствие было максимально точным. В итоге мы получили десятичную дробь, которая соответствует заданной точке на оси координат.

Выше мы приводили рисунок с точкой M . Посмотрите на него еще раз: чтобы попасть в эту точку, нужно отмерить от нуля один единичный отрезок и четыре десятых доли от его, поскольку этой точке соответствует десятичная дробь 1 , 4 .

Если мы не можем попасть в точку в процессе десятичного измерения, то значит, что ей соответствует бесконечная десятичная дробь.