Момент инерции сплошного цилиндра формула

Момент инерции однородного сплошного цилиндра радиуса R относительно его геометрической оси__

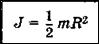
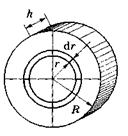Разобьем цилиндр на отдельные полые концент­рические цилиндры бесконечно малой толщины dr с внутренним радиусом rи внешним (r+ dr). Момент инерции каждого полого цилиндра dJ = r 2 dm (dr 3 · dr (p — плотность материала). Момент инерции сплошного цилиндра

.

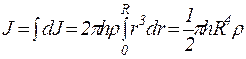
Поскольку πR 2 h — объем цилиндра, его масса т = πR 2 hp, а .

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8944 — | 7612 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Как известно, масса в динамике поступательного движения играет важную роль, определяя инерционные свойства движущихся тел. В динамике вращения вместо массы пользуются моментом инерции. Рассмотрим в статье, что это за величина и как определяется момент инерции цилиндра относительно оси.

Что такое момент инерции?

Эту величину обычно обозначают буквой I. Для материальной точки математическая формула момента инерции записывается так:

Где r — расстояние до оси вращения от точки массой m. Из формулы понятно, что единицей измерения величины являются килограммы на квадратный метр (кг*м 2 ).

Если тело имеет сложную форму и его объемная плотность является переменной, тогда для определения I следует использовать такое интегральное выражение:

Где dm — это элементарная масса, находящаяся от оси вращения на расстоянии r.

Таким образом, момент инерции определяет распределение материи в теле сложной формы относительно конкретной оси вращения системы.

Сплошной цилиндр и главная ось

Момент инерции сплошного цилиндра может быть вычислен вокруг абсолютно любой оси с использованием интегрального выражения, записанного в предыдущем пункте. Здесь рассмотрим ситуацию, когда цилиндр массой M, радиусом R и высотой L вращается вокруг главной оси. Последняя представляет собой прямую, параллельную генератрисе фигуры и проходящую через центры ее круглых оснований.

Не будем вдаваться в подробности математических вычислений по интегральной формуле, а приведем сразу конечное выражение:

Мы видим, что чем больше масса цилиндра и его радиус, тем больше момент инерции I₁. В то же время эта величина никак не зависит от высоты фигуры L, то есть момент инерции тонкого диска можно вычислить также по этой формуле.

Отметим, что если всю массу цилиндра собрать в одну материальную точку, находящуюся от оси вращения на расстоянии радиуса R, то для нее момент инерции окажется в два раза больше, чем для сплошного цилиндра.

Однородный цилиндр и перпендикулярная генератрисе ось

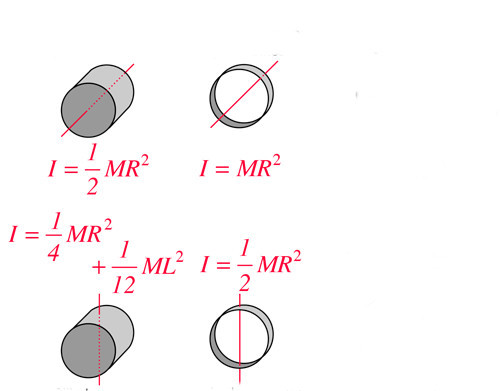
Теперь возьмем однородный цилиндр из примера выше и перевернем его на бок. Начнем вращать объект вокруг оси, которая проходит также через центр его масс, но уже перпендикулярна генератрисе (главной оси). Чему будет равен момент инерции цилиндра однородного в данном случае?

Как и в примере выше, здесь также ограничимся приведением соответствующего выражения. Оно будет иметь следующий вид:

Момент инерции I₂ имеет более сложную зависимость от параметров цилиндра, чем I₁, поскольку он определяется не только массой и радиусом, но и высотой фигуры. Заметим, что два слагаемых этой формулы представляют собой два крайних случая:

• Если цилиндр слишком маленькую высоту имеет, то мы получаем диск, который, вращаясь вокруг оси, проходящей через его диаметр, будет иметь момент 1/4*M*R 2 .
• Если радиус цилиндра стремится к нулю, то рассматриваемый объект превратится в стержень, и его момент инерции станет равным 1/12*M*L 2 .

Полый цилиндр

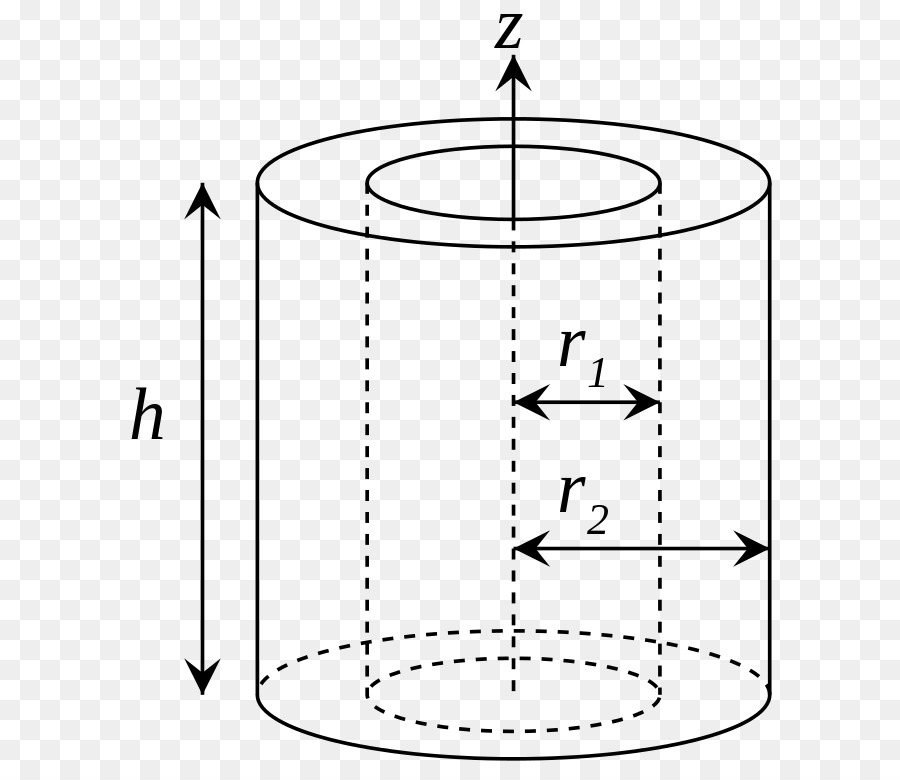
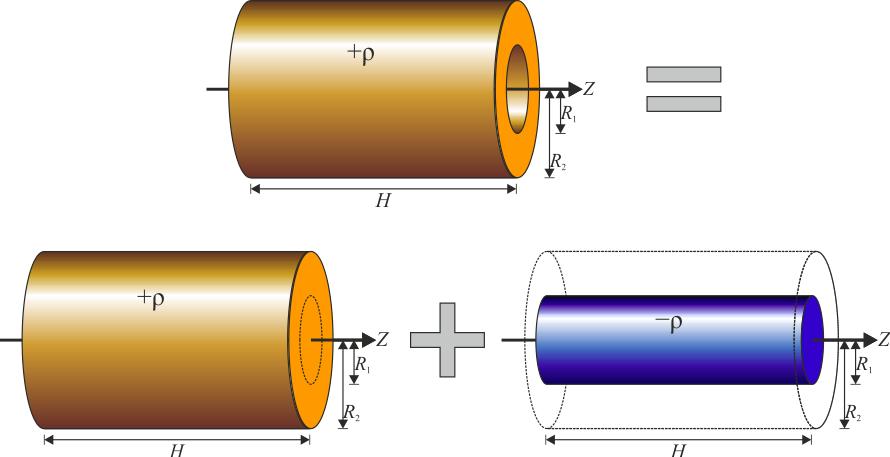
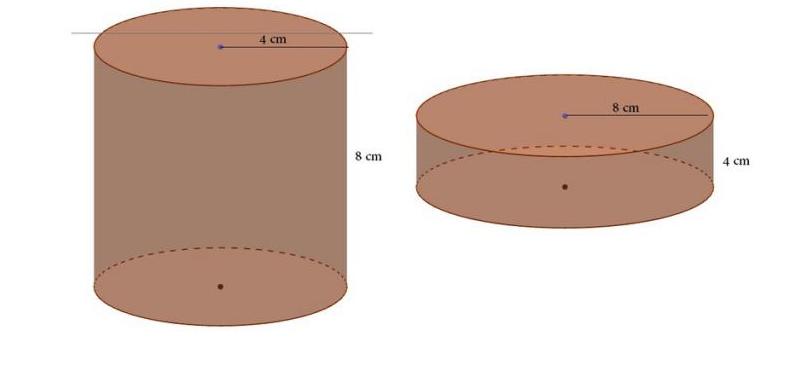
Выше мы рассмотрели, как рассчитывать момент инерции цилиндра вращающегося и однородного. Теперь предположим, что высота цилиндра и его масса остались теми же самыми, однако он стал полым, то есть, имеет два радиуса: внешний R₁ и внутренний R₂.

Применение все той же интегральной формулы позволяет получить выражение для момента инерции цилиндра полого, который вращается вокруг своей главной оси. Соответствующая формула выглядит так:

Это выражение позволяет сделать важный вывод: при одинаковых массах полого и сплошного цилиндров первый обладает большим моментом инерции. Связан этот факт с тем, что большая часть массы полого цилиндра находится дальше от оси вращения, а как видно из формул, от радиуса изучаемая величина растет квадратично.

Где используются знания величин I для цилиндров?

Пожалуй, основной областью применения изложенной выше теории является автомобильная промышленность. В частности, коленчатый вал автомобиля снабжен тяжелым сплошным маховиком, имеющим цилиндрическую форму. Необходим маховик для того, чтобы обеспечить максимальную плавность вращения коленчатого вала, что отражается на плавности автомобильного хода. Маховик гасит любые большие угловые ускорения как во время разгона транспортного средства, так при его торможении.

Из формулы выше для момента инерции I₁ понятно, что для увеличения этой величины выгоднее увеличить радиус, чем массу цилиндра (маховика). Так, удвоение массы приведет лишь к удвоению момента инерции. Однако если увеличить в два раза радиус, то I₁ возрастет аж в 4 раза, что обеспечит более эффективное использование маховика.

Пример решения задачи

Прежде чем решать задачу, скажем несколько слов о динамике вращения. Как и в динамике поступательного движения, в ней существует формула, подобная второму закону Ньютона. Эта формула называется уравнением моментов. Записывается она так:

Где L — момент импульса, M — момент внешних сил. Чаще всего это уравнение записывают в следующем виде:

Здесь α — ускорение угловое. Из этого выражения видна аналогия со вторым ньютоновским законом.

Теперь перейдем к решению задачи. Известно, что сила в 100 Н действует по касательной к цилиндрической поверхности перпендикулярно главной оси вращения сплошного цилиндра на расстоянии 20 см. Масса цилиндра равна 10 кг, а его радиус составляет 20 см. Необходимо определить угловую скорость ω цилиндра через 5 секунд после начала действия силы.

Угловая скорость рассчитывается по формуле для равноускоренного движения:

Выражая ускорение из уравнения моментов и подставляя его в выражение, получим:

Момент силы вычисляется так:

Где по условию задачи d = R. Подставляя это выражение и выражение для I сплошного цилиндра, получим конечную рабочую формулу:

Осталось сюда подставить все величины в единицах СИ и записать ответ: ω = 500 рад/с, что равно приблизительно 80 оборотам в секунду.

Осевые моменты инерции некоторых тел

Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения

Материальная точка массы m

На расстоянии r от точки, неподвижная

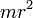
Полый тонкостенный цилиндр или кольцо радиуса r и массы m

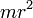
Сплошной цилиндр или диск радиуса r и массы m

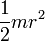
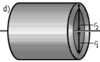
Полый толстостенный цилиндр массы m с внешним радиусом r₂ и внутренним радиусом r₁

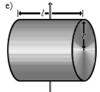
Сплошной цилиндр длины l, радиуса r и массы m

Ось перпендикулярна к цилиндру и проходит через его центр масс

Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m

Ось перпендикулярна к цилиндру и проходит через его центр масс

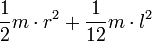
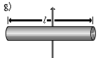
Прямой тонкий стержень длины l и массы m

Ось перпендикулярна к стержню и проходит через его центр масс

Тонкостенная сфера радиуса r и массы m

Ось проходит через центр сферы

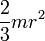
Шар радиуса r и массы m

Ось проходит через центр шара

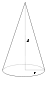
Конус радиуса r и массы m

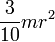
Равнобедренный треугольник с высотой h, основанием a и массой m

Ось перпендикулярна плоскости треугольника и проходит через вершину

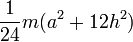
Правильный треугольник со стороной a и массой m

Ось перпендикулярна плоскости треугольника и проходит через центр масс

Квадрат со стороной a и массой m

Ось перпендикулярна плоскости квадрата и проходит через центр масс

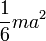
Тонкостенный цилиндр (кольцо, обруч)

Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJ_i. Тогда

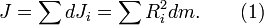
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду

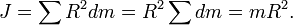
Толстостенный цилиндр (кольцо, обруч)

Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R₁, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит

Момент инерции толстого кольца найдём как интеграл

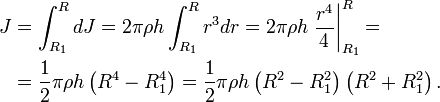
Поскольку объём и масса кольца равны

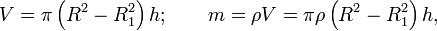
получаем окончательную формулу для момента инерции кольца

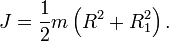
Однородный диск (сплошной цилиндр)

Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R₁ = 0), получим формулу для момента инерции цилиндра (диска):

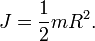
Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен

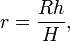
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят

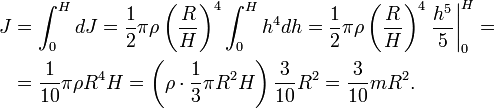
Сплошной однородный шар

Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле

Масса и момент инерции такого диска составят

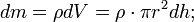
Момент инерции сферы найдём интегрированием:

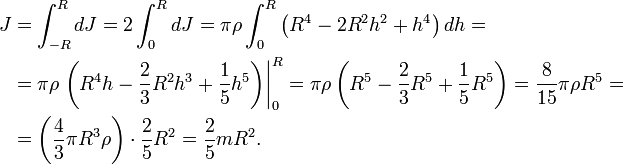
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:

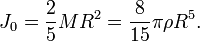
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.

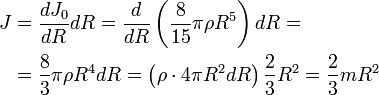
Тонкий стержень (ось проходит через центр)

Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна

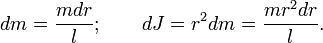
Тонкий стержень (ось проходит через конец)

При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен