Матрица размера mxn называется

Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.

Матрица порядка m × n записывается в форме:

или (i=1,2. m; j=1,2. n).

Числа a_ij входящие в состав данной матрицы называются ее элементами. В записи a_ij первый индекс i означает номер строки, а второй индекс j— номер столбца.

Матрица строка

Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:

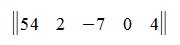
Матрица столбец

Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например

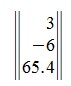
Нулевая матрица

Если все элементы матрицы равны нулю,то матрица называется нулевой матрицей . Например

Квадратная матрица

Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:

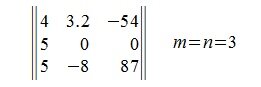
Главная диагональ матрицы

Элементы расположенные на местах a 11, a 22 . a_nn образуют главную диагональ матрицы. Например:

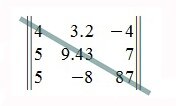
В случае m×n -матриц элементы a_ii ( i= 1,2. min(m,n)) также образуют главную диагональ. Например:

Элементы расположенные на главной диагонали называются главными диагональными элементами или просто диагональными элементами .

Побочная диагональ матрицы

Элементы расположенные на местах a 1n, a 2n-1 . a n1 образуют побочную диагональ матрицы. Например:

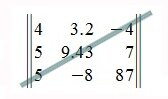
Диагональная матрица

Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:

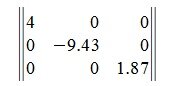
Единичная матрица

Квадратную матрицу n-го порядка, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю, называется единичной матрицей и обозначается через E или E n , где n — порядок матрицы. Единичная матрица порядка 3 имеет следующий вид:

След матрицы

Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:

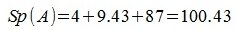
Верхняя треугольная матрица

Квадратная матрица порядка n×n называется верхней треугольной матрицей, если равны нулю все элементы матрицы, расположенные под главной диагональю, т.е. a_ij=0, при всех i>j . Например:

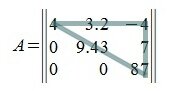
Нижняя треугольная матрица

Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. a_ij=0, при всех i T ).

Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).

Ядро или нуль пространство матрицы

Множесто всех решений уравнения Ax=0, где A- mxn-матрица, x— вектор длины n — образует нуль пространство или ядро матрицы A и обозначается через Ker(A) или N(A).

Противоположная матрица

Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.

Кососимметричная (Кососимметрическая) матрица

Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:

В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.

Пример кососимметрической матрицы:

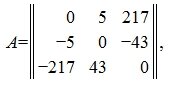
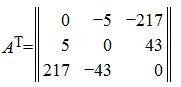
Разность матриц

Разностью C двух матриц A и B одинакового размера определяется равенством

Для обозначения разности двух матриц используется запись:

Степень матрицы

Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:

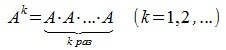
где E-единичная матрица.

Из сочетательного свойства умножения следует:

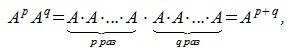
где p,q— произвольные целые неотрицательные числа.

Симметричная (Симметрическая) матрица

Матрица, удовлетворяющая условию A=A T называется симметричной матрицей.

Для симметричных матриц имеет место равенство:

Прямоугольной матрицей размера mxn называется совокупность mxn чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов. Мы будем записывать ее в виде

(4.1)

или сокращенно в виде A = (a_{i j}) (i =; j = ), числа a_{i j}, называются ее элементами; первый индекс указывает на номер строки, второй — на номер столбца. A = (a_{i j}) и B = (b_{i j}) одинакового размера называются равными, если попарно равны их элементы, стоящие на одинаковых местах, то есть A = B, если a_{i j} = b_{i j}.

Матрица, состоящая из одной строки или одного столбца, называется соответственно вектор-строкой или вектор-столбцом. Вектор-столбцы и вектор-строки называют просто векторами.

Матрица, состоящая из одного числа, отождествляется с этим числом. A размера mxn, все элементы которой равны нулю, называются нулевой и обозначается через 0. Элементы с одинаковыми индексами называют элементами главной диагонали. Если число строк равно числу столбцов, то есть m = n, то матрицу называют квадратной порядка n. Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными и записываются так:

.

Если все элементы a_{i i} диагонали равны 1, то она называется единичной и обозначается буквой Е:

.

Квадратная матрица называется треугольной, если все элементы, стоящие выше (или ниже) главной диагонали, равны нулю. Транспонированием называется такое преобразование , при котором строки и столбцы меняются местами с сохранением их номеров. Обозначается транспонирование значком Т наверху.

Если в (4.1) переставим строки со столбцами, то получим

,

которая будет транспонированной по отношению к А. В частности, при транспонировании вектора-столбца получается вектор-строка и наоборот.

Произведением А на число b называется матрица, элементы которой получаются из соответствующих элементов А умножением на число b: b A = (b a_{i j}).

Суммой А = (a_{i j}) и B = (b_{i j}) одного размера называется C = (c_{i j}) того же размера, элементы которой определяются по формуле c_{i j} = a_{i j} + b_{i j}.

Произведение АВ определяется в предположении, что число столбцов А равно числу строк В.

Произведением AB, где А = (a_{i j}) и B = (b_{j k}), где i =, j=, k=, заданных в определенном порядке АВ, называется С = (c _{i k}), элементы которой определяются по следующему правилу:

c _{i k} = a_{i 1} b_{1 k} + a_{i 2} b_{2 k} +. + a_{i m} b_{m k} = a_{i s} b_{s k}. (4.2)

Иначе говоря, элемент произведения AB определяются следующим образом: элемент i-й строки и k-го столбца С равен сумме произведений элементов i-й строки А на соответствующие элементы k-го столбца В.

Пример 2.1. Найти произведение AB и .

Решение. Имеем: А размера 2×3, В размера 3×3, тогда произведение АВ = С существует и элементы С равны

с₁₁ = 1×1 +2×2 + 1×3 = 8, с₂₁ = 3×1 + 1×2 + 0×3 = 5, с₁₂ = 1×2 + 2×0 + 1×5 = 7,

с₂₂ =3×2 + 1×0 + 0×5 = 6, с₁₃ = 1×3 + 2×1 + 1×4 = 9, с₂₃ = 3×3 + 1×1 + 0×4 = 10.

, а произведение BA не существует.

Пример 2.2. В таблице указано количество единиц продукции, отгружаемой ежедневно на молокозаводах 1 и 2 в магазины М₁, М₂ и М₃, причем доставка единицы продукции с каждого молокозавода в магазин М₁ стоит 50 ден. ед., в магазин М₂ — 70, а в М₃ — 130 ден. ед. Подсчитать ежедневные транспортные расходы каждого завода.

Определение 6.Матрицей размера mxn называется прямоугольная таблица чисел , i= 1,2, … ,m, j= 1,2, …, n, состоящая из m строк и n столбцов.

А =

Определение 7.Суммой А+В (mxn) — матриц A = ( и B = ( 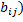называется матрица C( того же порядка, каждый элемент который равен сумме соответственных элементов матриц A и B: 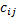= + 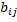, i=1,2, …, m, j= 1,2, … ,n.

Определение 8.Произведением αА матрицы А=( ) на действительное число α называется матрица B= ( 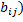, получающаяся из матрицы А умножением всех её элементов на 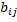α: =α , i=1,2, … ,m , j= 1,2, … ,n.

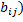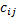Определение9.Произведением АВ (mxn) –матрицы А =( на (nxk) –матрицу B=( называется (mxk)- матрица C( , элемент которой , состоящий вi-й строке и j-м столбце, равен сумме произведений соответственных элементов i-й строки матрицы А и j-го столбца матрицы

B: = 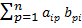, i=1,2,…,m, j=1,2,…,k.

Матрицы перемножить возможно тогда, когда число столбцов матрицы А равно числу строк В. Для матриц одинакового размера справедливы свойства следующих алгебраических операций:

Определение 10.Нуль-матрицей называется матрица О, все элементы которой равны нулю.

Определение 11.Единичной матрицей Е называется квадратная матрица , на главной диагонали которой стоят единицы, а остальные элементы равны нулю.

Например, Е= .

Справедливы равенства : А+О=А; АЕ=ЕА=А.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10219 — | 7588 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно