Назначение сервиса . С помощью данного сервиса можно в онлайн режиме решить задачу линейного программирования геометрическим методом, а также получить решение двойственной задачи (оценить оптимальность использования ресурсов). Дополнительно создается шаблон решения в Excel .
- Решение онлайн
- Видеоинструкция
- Оформление Word
- Также решают
Решение задачи линейного программирования графическим методом включает следующие этапы:
- На плоскости X10X2 строят прямые.
- Определяются полуплоскости.
- Определяют многоугольник решений;
- Строят вектор N(c1,c2), который указывает направление целевой функции;
- Передвигают прямую целевую функцию c1x2 + c2x2 = 0 в направлении вектора N до крайней точки многоугольника решений.
- Вычисляют координаты точки и значение целевой функции в этой точке.
Пример . Компания изготавливает два вида продукции – П1 и П2. Для производства продукции используются два вида сырья – С1 и С2. Оптовые цены единицы продукции равна: 5 д.е. для П1 и 4 д.е. для П2. Расход сырья на единицу продукции вида П1 и вида П2 дан в таблице.
Таблица — Расход сырья на производство продукции
| Сырье | Расход сырья на 1 ед. продукции | Максимальный запас сырья, ед. | |
| П1 | П2 | ||
| М1 | 6 | 4 | 24 |
| М2 | 1 | 2 | 6 |
Установлены ограничения на спрос продукции: ежедневный объем производства продукции П2 не должен превышать ежедневный объем производства продукции П1 не более чем на 1 тонну; максимальный ежедневный объем производства П2 не должен превышать 2 т.
Требуется определить:
Какое количество продукции каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным?
- Сформулировать математическую модель задачи линейного программирования.
- Решить задачу линейного программирования графическим способом (для двух переменных).
Решение.
Сформулируем математическую модель задачи линейного программирования.
x1 – производство продукции П1, ед.
x2 – производство продукции П2, ед.
x1, x2 ≥ 0
Если количество переменных в задаче линейного программирования больше двух, то задачу предварительно сводят к стандартной ЗЛП.
F(X) = 3x1 — 2x2 + 5x3 — 4x5 → max при ограничениях:
x1 + x2 + x3=12
2x1 — x2 + x4=8
— 2x1 + 2x2 + x5=10
F(X) = 3x1 — 2x2 + 5x3 — 4x5
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:
| 1 | 1 | 1 | 12 | ||
| 2 | -1 | 1 | 8 | ||
| -2 | 2 | 1 | 10 |
Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x3.
2. В качестве базовой переменной можно выбрать x4.
3. В качестве базовой переменной можно выбрать x5.
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x1 + x2 + x3 = 12
2x1 — x2 + x4 = 8
— 2x1 + 2x2 + x5 = 10
Выразим базисные переменные через остальные:
x3 = — x1 — x2+12
x4 = — 2x1 + x2+8
x5 = 2x1 — 2x2+10
Подставим их в целевую функцию:
F(X) = 3x1 — 2x2 + 5(- x1 — x2+12) — 4(2x1 — 2x2+10)
или
F(X) = — 10x1 + x2+20 → max
Система неравенств:
— x1 — x2+12 ≥ 0
— 2x1 + x2+8 ≥ 0
2x1 — 2x2+10 ≥ 0
Приводим систему неравенств к следующему виду:
x1 + x2 ≤ 12
2x1 — x2 ≤ 8
— 2x1 + 2x2 ≤ 10
F(X) = — 10x1 + x2+20 → max
Особенности решения задач линейного программирования графическим методом
Переменную x2 принимаем в качестве дополнительной переменной и делаем замену на знак «≥»:
f=x1 + 6x3+ 27
x1 + 3x3≥6
Далее задача решается графическом способом.
Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Московский государственный университет технологий и управления имени К.Г. Разумовского»
Филиал ФГБОУ ВПО «МГУТУ имени К.Г. Разумовского» в г. Мелеузе (Республика Башкортостан)
графический метод решения задач линейного программирования
для заочной формы обучения по квалификации
220700.62 по направлению Автоматизация технологических процессов
151000.62 по направлению Технологические машины и оборудование
260100.62 по направлению Продукты питания из растительного сырья (технология консервов и пищеконцентратов, технология хранения зерна)
ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Графический метод решения задач линейного программирования с двумя переменными
Графический метод используется для решения задач с двумя переменными следующего вида:
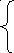a11x1 + a12x2≤(≥) b1,
Данный метод основывается на возможности графического изображения области допустимых решений задачи и нахождении среди них оптимального решения.
Область допустимых решений задачи строится как пересечение (общая часть) областей решений каждого из заданных ограничений (2), (3).
Для того чтобы определить, какая из двух координатных полуплоскостей является областью решений, достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство: если оно удовлетворяется, то областью решений является полуплоскость, содержащая данную точку, если же неравенство не удовлетворяется, то областью Решений является полуплоскость, не содержащая данную точку.
Областью допустимых решений задачи является общая часть полуплоскостей — областей решений всех неравенств системы ограничений.
Для нахождения среди допустимых решений оптимального решения. Используют линии уровня и опорные прямые.
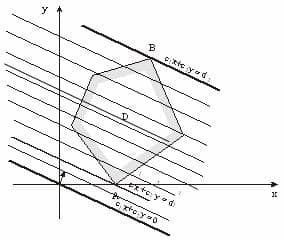
Линией уровня называется прямая, на которой целевая функция задачи принимает постоянное значение. Уравнение линии уровня в общем имеет вид с1х1 + с2х2 = l, где l = const. Все линии уровня параллельны между собой. Их нормаль ñ = (с1, с2).
Опорной прямой называется линия уровня, которая имеет хотя бы одну общую точку с областью допустимых решений и по отношению, к которой эта область находится в одной из полуплоскостей.
Область допустимых решений любой задачи имеет не более двух опорных прямых, на одной из которых может находиться оптимальное решение (рис. 29.1).
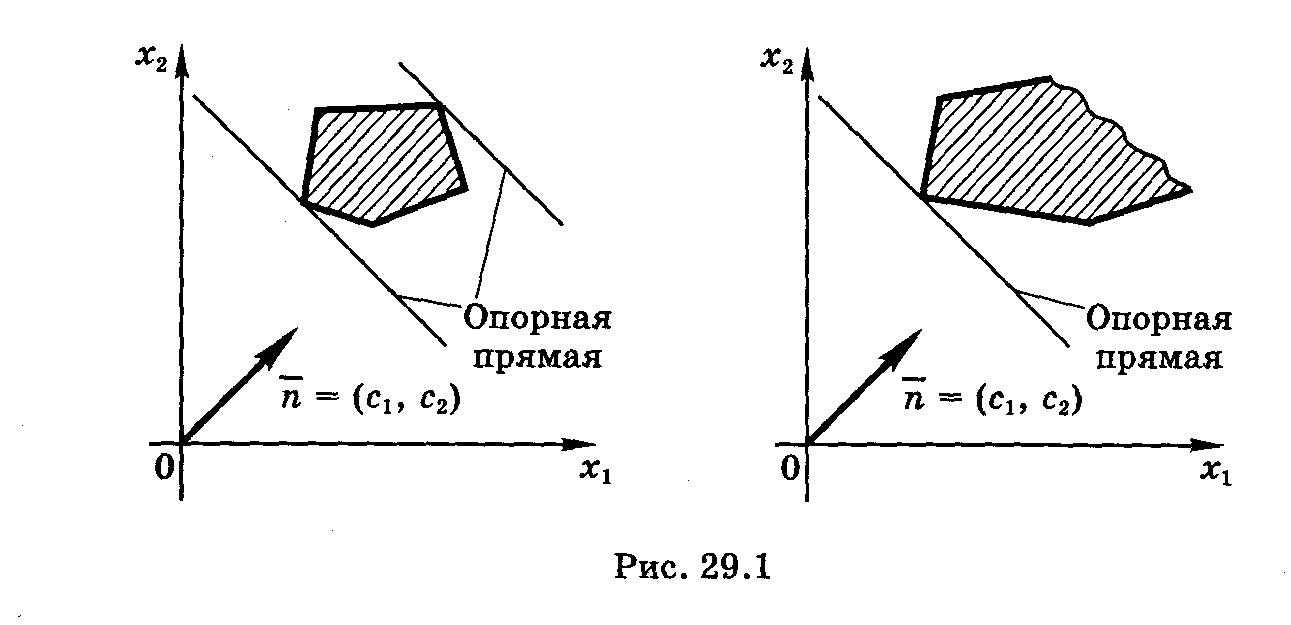
Значения целевой функции на линиях уровня возрастают, если линии уровня перемещать в направлении их нормали, и убывают при перемещении линий уровня в противоположном направлении.
Алгоритм графического метода решения задач линейного программирования с двумя переменными:
1.Построить область допустимых решений.
2.Если область допустимых решений является пустым множеством, то задача не имеет решения ввиду несовместности системы ограничений.
3.Если область допустимых решений является непустым множеством, построить нормаль линий уровня ñ = (c1,c2) и одну из линий уровня, имеющую общие точки с этой областью.
4.Линию уровня переместить до опорной прямой в задаче на максимум в направлении нормали, в задаче на минимум — в противоположном направлении.
5.Если при перемещении линии уровня по области допустимых решений в направлении, соответствующем приближению к экстремуму целевой функции, линия уровня уходит в бесконечность, то задача не имеет решения ввиду неограниченности целевой функции.
6.Если задача линейного программирования имеет оптимальное решение, то для его нахождения решить совместно уравнения прямых, ограничивающих область допустимых решений и имеющих общие точки с соответствующей опорной прямой. Если целевая функция задачи достигает экстремума в двух угловых точках, то задача имеет бесконечное множество решений. Оптимальным решением является любая выпуклая линейная комбинация этих точек. После нахождения оптимальных решений вычислить значение целевой функции на этих решениях.
1. Решить задачу линейного программирования
x1 — x2 + 2≥0, (1)
Р
ешение. Строим область допустимых решений задачи. Нумеруем ограничения задачи. В прямоугольной декартовой системе координат (рис. 29.2) строим прямую х1 — х2 + 2 = 0 (L1), соответствующую ограничению (1). Находим, какая из двух полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1). Для этого достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство. Так как прямая L1 не проходит через начало координат, подставляем координаты точки О (0, 0) в первое ограничение 1•0—1•0+2≥0. Получаем строгое неравенство 2>0. Следовательно, точка О лежит в полуплоскости решений. Таким образом, стрелки на концах прямой L1 должны быть направлены в полуплоскость, содержащую точку О. Аналогично строим прямые Зх1 — 2х2 — 6 = 0 (L2), 2х1 + х2 — 2 = 0 (L3), х2 = 3 (L4) и области решений ограничений (2), (3) и (4). Находим общую часть полуплоскостей решений, учитывая при этом условия неотрицательности; полученную область допустимых решений отметим на рис. 29.2 штриховкой.
Строим нормаль линий уровня ñ = (3, 2) и одну из этих линий, например 3х1 + 2х2 = 0. Так как решается задача на отыскание максимума целевой функции, то линию уровня перемещаем в направлении нормали до опорной прямой. Эта прямая проходит через точку X * пересечения прямых, ограничивающих область допустимых решений и соответствующих неравенствам (2) и (4). Определяем, координаты точки X * =L2∩L4.
Р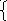
ешая систему 3x1 – 2x2 – 6 = 0, получаем X * = (4, 3).
Вычисляем Z(X * ) = 3 • 4 + 2 • 3 = 18.
2. Решить задачу линейного программирования
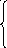4x1 – x2 ≥ 0 (1)
Р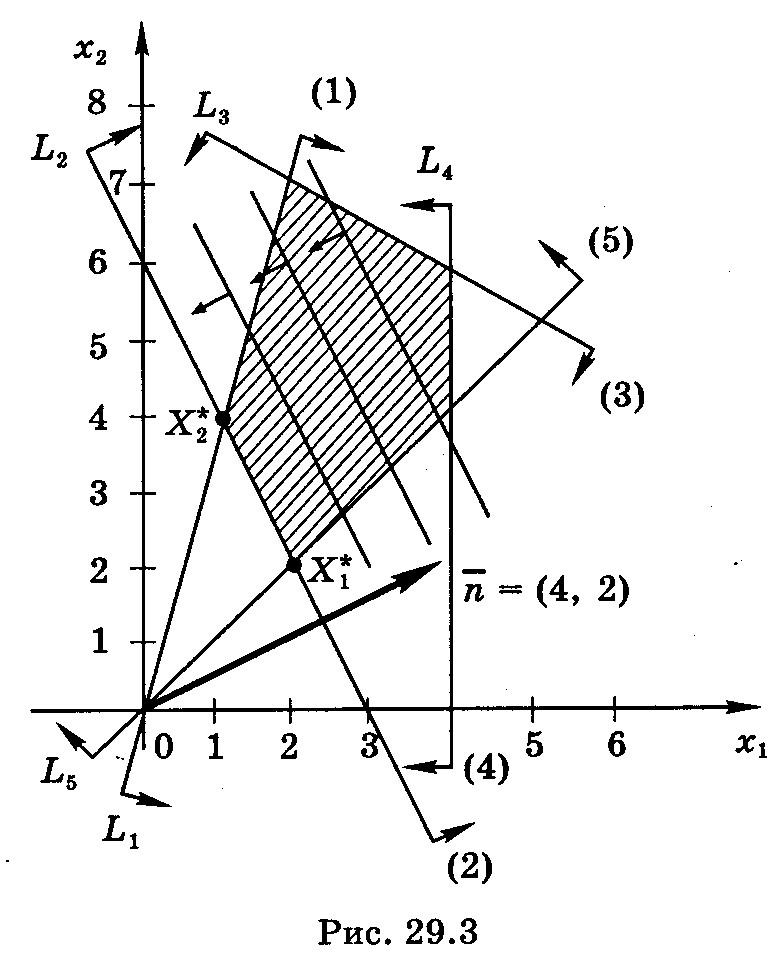
ешение. Строим область допустимых решений, нормаль линий уровня ñ = (4, 2) и одну из линий уровня, имеющую общие точки с этой областью (рис. 29.3). Перемещаем линию уровня в направлении, противоположном направлению нормали ñ , так как решается задача на отыскание минимума функции Нормаль линий уровня ñ 2 = (4, 2) и нормаль ñ2 = (2, 1) граничной прямой L2, в направлении которой перемещаются линии уровня, параллельны, так как их координаты пропорциональны (4 : 2 = 2 : 1). Следовательно, опорная прямая совпадает с граничной прямой L2 области допустимых решений и проходит через две угловые точки этой области X1 * и Х2 * • Задача имеет бесконечное множество оптимальных решений, являющихся точками отрезка [X1 * , Х2 * ].Эти точки Х1 * =L2∩L5, Х2 * =L1∩L2 находим, решая соответствующие системы уравнений:
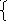2x1 + x2 =6, (L1) 4x1 – x2=0, (L1)
3. Решить задачу линейного программирования
5x1 – x2 ≥ 0, (1)
Р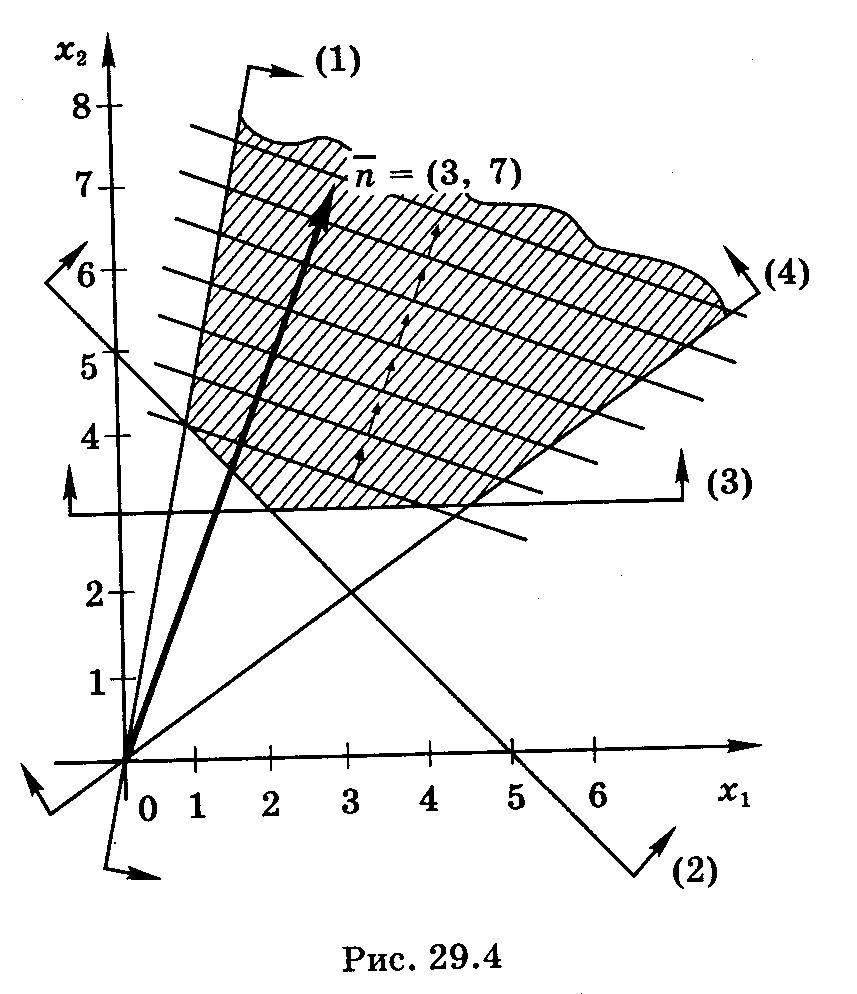
ешение. Строим область допустимых решений, нормаль ñ = (3, 7) и одну из линий уровня (рис. 29.4).
В данной задаче необходимо найти максимум целевой функции, поэтому линию уровня перемещаем в направлении нормали. Ввиду того, что в этом направлении область допустимых решений не ограничена, линия уровня уходит в бесконечность. Задача не имеет решения вследствие неограниченности целевой функции.
4. Решить задачу линейного программирования
3
x1 – x2 ≥ 0, (1)
Р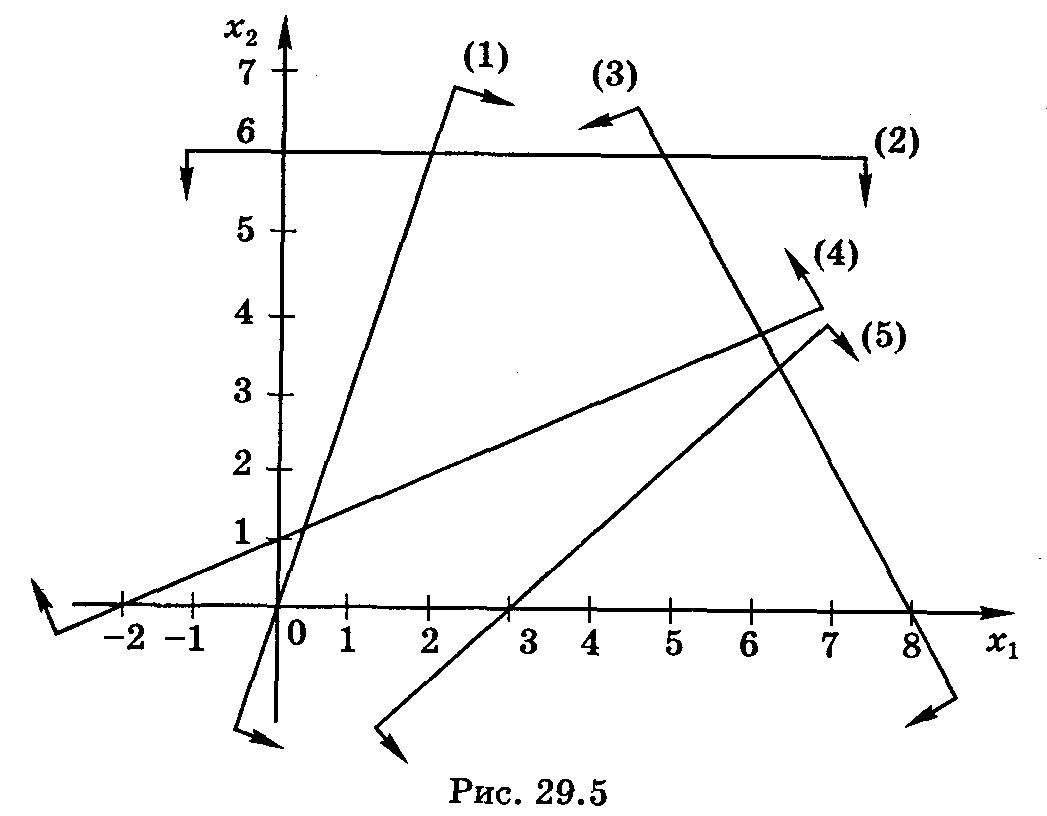
ешение. Строим прямые линии, соответствующие неравенствам системы ограничений и находим полуплоскости, являющиеся областями решений этих неравенств (рис. 29.5).
Область допустимых решений задачи является пустым множеством. Задача не имеет решения ввиду несовместности системы ограничений.
Ответ: система ограничений несовместна.
Ранее я описал, как принимать решения с учетом ограничивающих факторов. Цель таких решений – определить ассортимент продукции (производственный план), максимально увеличивающий прибыль компании. Решение заключалось в том, чтобы распределить ресурсы между продуктами согласно маржинальной прибыли, полученной на единицу ограниченных ресурсов, при соблюдении любых других ограничений, таких как максимальный или минимальный спрос на отдельные виды продукции. [1]
Если ограничивающий фактор один (например, дефицитный станок), решение может быть найдено с применением простых формул (см. ссылку в начале статьи). Если же ограничивающих факторов несколько, применяется метод линейного программирования.
Линейное программирование – это название, данное комбинации инструментов используемых в науке об управлении. Этот метод решает проблему распределения ограниченных ресурсов между конкурирующими видами деятельности с тем, чтобы максимизировать или минимизировать некоторые численные величины, такие как маржинальная прибыль или расходы. В бизнесе он может использоваться в таких областях как планирование производства для максимального увеличения прибыли, подбор комплектующих для минимизации затрат, выбор портфеля инвестиций для максимизации доходности, оптимизация перевозок товаров в целях сокращения расстояний, распределение персонала с целью максимально увеличить эффективность работы и составление графика работ в целях экономии времени.
Скачать заметку в формате Word, рисунки в формате Excel
Линейное программирование предусматривает построение математической модели рассматриваемой задачи. После чего решение может быть найдено графически (рассмотрено ниже), с использованием Excel (будет рассмотрено отдельно) или специализированных компьютерных программ. [2]
Пожалуй, построение математической модели – наиболее сложная часть линейного программирования, требующая перевода рассматриваемой задачи в систему переменных величин, уравнений и неравенств – процесс, в конечном итоге зависящий от навыков, опыта, способностей и интуиции составителя модели.
Рассмотрим пример построения математической модели линейного программирования
Николай Кузнецов управляет небольшим механическим заводом. В будущем месяце он планирует изготавливать два продукта (А и В), по которым удельная маржинальная прибыль оценивается в 2500 и 3500 руб., соответственно.
Изготовление обоих продуктов требует затрат на машинную обработку, сырье и труд (рис. 1). На изготовление каждой единицы продукта А отводится 3 часа машинной обработки, 16 единиц сырья и 6 единиц труда. Соответствующие требования к единице продукта В составляют 10, 4 и 6. Николай прогнозирует, что в следующем месяце он может предоставить 330 часов машинной обработки, 400 единиц сырья и 240 единиц труда. Технология производственного процесса такова, что не менее 12 единиц продукта В необходимо изготавливать в каждый конкретный месяц.
Рис. 1. Использование и предоставление ресурсов
Николай хочет построить модель с тем, чтобы определить количество единиц продуктов А и В, которые он доложен производить в следующем месяце для максимизации маржинальной прибыли.
Линейная модель может быть построена в четыре этапа.
Этап 1. Определение переменных
Существует целевая переменная (обозначим её Z), которую необходимо оптимизировать, то есть максимизировать или минимизировать (например, прибыль, выручка или расходы). Николай стремится максимизировать маржинальную прибыль, следовательно, целевая переменная:
Z = суммарная маржинальная прибыль (в рублях), полученная в следующем месяце в результате производства продуктов А и В.
Существует ряд неизвестных искомых переменных (обозначим их х1, х2, х3 и пр.), чьи значения необходимо определить для получения оптимальной величины целевой функции, которая, в нашем случае является суммарной маржинальной прибылью. Эта маржинальная прибыль зависит от количества произведенных продуктов А и В. Значения этих величин необходимо рассчитать, и поэтому они представляют собой искомые переменные в модели. Итак, обозначим:
х1 = количество единиц продукта А, произведенных в следующем месяце.
х2 = количество единиц продукта В, произведенных в следующем месяце.
Очень важно четко определить все переменные величины; особое внимание уделите единицам измерения и периоду времени, к которому относятся переменные.
Этап. 2. Построение целевой функции
Целевая функция – это линейное уравнение, которое должно быть или максимизировано или минимизировано. Оно содержит целевую переменную, выраженную с помощью искомых переменных, то есть Z выраженную через х1, х2… в виде линейного уравнения.
В нашем примере каждый изготовленный продукт А приносит 2500 руб. маржинальной прибыли, а при изготовлении х1 единиц продукта А, маржинальная прибыль составит 2500 * х1. Аналогично маржинальная прибыль от изготовления х2 единиц продукта В составит 3500 * х2. Таким образом, суммарная маржинальная прибыль, полученная в следующем месяце за счет производства х1 единиц продукта А и х2 единиц продукта В, то есть, целевая переменная Z составит:
Николай стремится максимизировать этот показатель. Таким образом, целевая функция в нашей модели:
Максимизировать Z = 2500 * х1 + 3500 *х2
Этап. 3. Определение ограничений
Ограничения – это система линейных уравнений и/или неравенств, которые ограничивают величины искомых переменных. Они математически отражают доступность ресурсов, технологические факторы, условия маркетинга и иные требования. Ограничения могут быть трех видов: «меньше или равно», «больше или равно», «строго равно».
В нашем примере для производства продуктов А и В необходимо время машинной обработки, сырье и труд, и доступность этих ресурсов ограничена. Объемы производства этих двух продуктов (то есть значения х1 их2) будут, таким образом, ограничены тем, что количество ресурсов, необходимых в производственном процессе, не может превышать имеющееся в наличии. Рассмотрим ситуацию со временем машинной обработки. Изготовление каждой единицы продукта А требует трех часов машинной обработки, и если изготовлено х1, единиц, то будет потрачено З * х1, часов этого ресурса. Изготовление каждой единицы продукта В требует 10 часов и, следовательно, если произведено х2 продуктов, то потребуется 10 * х2 часов. Таким образом, общий объем машинного времени, необходимого для производства х1 единиц продукта А и х2 единиц продукта В, составляет 3 * х1 + 10 * х2. Это общее значение машинного времени не может превышать 330 часов. Математически это записывается следующим образом:
Аналогичные соображения применяются к сырью и труду, что позволяет записать еще два ограничения:
Наконец следует отметить, что существует условие, согласно которому должно быть изготовлено не менее 12 единиц продукта В:
Этап 4. Запись условий неотрицательности
Искомые переменные не могут быть отрицательными числами, что необходимо записать в виде неравенств х1 ≥ 0 и х2 ≥ 0. В нашем примере второе условия является избыточным, так как выше было определено, что х2 не может быть меньше 12.
Полная модель линейного программирования для производственной задачи Николая может быть записана в виде:
Максимизировать: Z = 2500 * х1 + 3500 *х2
При условии, что: 3 * х1 + 10 * х2 ≤ 330
Рассмотрим графический метод решения задачи линейного программирования.
Этот метод подходит только для задач с двумя искомыми переменными. Модель, построенная выше, будет использована для демонстрации метода.
Оси на графике представляют собой две искомые переменные (рис. 2). Не имеет значения, какую переменную отложить вдоль, какой оси. Важно выбрать масштаб, который в конечном итоге позволит построить наглядную диаграмму. Поскольку обе переменные должны быть неотрицательными, рисуется только I-й квадрант.
Рис. 2. Оси графика линейного программирования
Рассмотрим, например, первое ограничение: 3 * х1 + 10 * х2 ≤ 330. Это неравенство описывает область, лежащую ниже прямой: 3 * х1 + 10 * х2 = 330. Эта прямая пересекает ось х1 при значении х2 = 0, то есть уравнение выглядит так: 3 * х1 + 10 * 0 = 330, а его решение: х1 = 330 / 3 = 110
Аналогично вычисляем точки пересечения с осями х1 и х2 для всех условий-ограничений:
| Область допустимых значений | Граница допустимых значений | Пересечение с осью х1 | Пересечение с осью х2 |
| 3 * х1 + 10 * х2 ≤ 330 | 3 * х1 + 10 * х2 = 330 | х1 = 110; х2 = 0 | х1 = 0; х2 = 33 |
| 16 * х1 + 4 * х2 ≤ 400 | 16 * х1 + 4 * х2 = 400 | х1 = 25; х2 = 0 | х1 = 0; х2 = 100 |
| 6 * х1 + 6 * х2 ≤ 240 | 6 * х1 + 6 * х2 = 240 | х1 = 40; х2 = 0 | х1 = 0; х2 = 40 |
| х2 ≥ 12 | х2 = 12 | не пересекает; идет параллельно оси х1 | х1 = 0; х2 = 12 |
Графически первое ограничение отражено на рис. 3.
Рис. 3. Построение области допустимых решений для первого ограничения
Любая точка в пределах выделенного треугольника или на его границах будет соответствовать этому ограничению. Такие точки называются допустимыми, а точки за пределами треугольника называются недопустимыми.
Аналогично отражаем на графике остальные ограничения (рис. 4). Значения х1 и х2 на или внутри заштрихованной области ABCDE будут соответствовать всем ограничениям модели. Такая область называется областью допустимых решений.
Рис. 4. Область допустимых решений для модели в целом
Теперь в области допустимых решений необходимо определить значения х1 и х2, которые максимизируют Z. Для этого в уравнении целевой функции:
разделим (или умножим) коэффициенты перед х1 и х2 на одно и тоже число, так чтобы получившиеся значения попали в диапазон, отражаемый на графике; в нашем случае такой диапазон – от 0 до 120; поэтому коэффициенты можно разделить на 100 (или 50):
затем присвоим Z значение равное произведению коэффициентов перед х1 и х2 (25 * 35 = 875):
и, наконец, найдем точки пересечения прямой с осями х1 и х2:
| Уравнение целевой функции | Пересечение с осью х1 | Пересечение с осью х2 |
| 875 = 25х1 + 35х2 | х1 = 35; х2 = 0 | х1 = 0; х2 = 25 |
Нанесем это целевое уравнение на график аналогично ограничениям (рис. 5):
Рис. 5. Нанесение целевой функции (черная пунктирная линия) на область допустимых решений
Значение Z постоянно на всем протяжении линии целевой функции. Чтобы найти значения х1 и х2, которые максимизируют Z, нужно параллельно переносить линию целевой функции к такой точке в границах области допустимых решений, которая расположена на максимальном удалении от исходной линии целевой функции вверх и вправо, то есть к точке С (рис. 6).
Рис. 6. Линия целевой функции достигла максимума в пределах области допустимых решений (в точке С)
Можно сделать вывод, что оптимальное решение будет находиться в одной из крайних точек области принятия решения. В какой именно, будет зависеть от угла наклона целевой функции и от того, какую задачу мы решаем: максимизации или минимизации. Таким образом, не обязательно чертить целевую функцию – все, что необходимо, это определить значения х1 и х2 в каждой из крайних точек путем считывания с диаграммы или путем решения соответствующей пары уравнений. Найденные значения х1 и х2 затем подставляются в целевую функцию для расчета соответствующей величины Z. Оптимальным решением является то, при котором получена максимальная величина Z при решении задачи максимизации, и минимальная – при решении задачи минимизации.
Определим, например значения х1 и х2 в точке С. Заметим, что точка С находится на пересечении линий: 3х1 + 10х2 = 330 и 6х1 + 6х2 = 240. Решение этой системы уравнений дает: х1 = 10, х2 = 30. Результаты расчета для всех вершин области допустимых решений приведены в таблице:
| Точка | Значение х1 | Значение х2 | Z = 2500х1 + 3500х2 |
| А | 22 | 12 | 97 000 |
| В | 20 | 20 | 120 000 |
| С | 10 | 30 | 130 000 |
| D | 33 | 115 500 | |
| E | 12 | 42 000 |
Таким образом, Николай Кузнецом должен запланировать на следующий месяц производство 10 изделий А и 30 изделий В, что позволит ему получить маржинальную прибыль в размере 130 тыс. руб.
Кратко суть графического метода решения задач линейного программирования можно изложить следующим образом:
- Начертите на графике две оси, представляющие собою два параметра решения; нарисуйте только I-й квадрант.
- Определите координаты точек пересечения всех граничных условий с осями, подставляя в уравнения граничных условий поочередно значения х1 = 0 и х2 = 0.
- Нанести линии ограничений модели на график.
- Определите на графике область (называемую допустимой областью принятия решения), которая соответствует всем ограничениям. Если такая область отсутствует, значит, модель не имеет решения.
- Определите значения искомых переменных в крайних точках области принятия решения, и в каждом случае рассчитайте соответствующее значение целевой переменной Z.
- Для задач максимизации решение – точка, в которой Z максимально, для задач минимизации, решение – точка, в которой Z минимально.
[1] Настоящая заметка написана по материалам CIMA .
Комментарии: 3 комментария
Пожалуйста, помогите, не могу определить ограничения в задаче и построить ОДР.
Инвестор, располагающий суммой в 300 тыс. ден. ед., может вложить свой капитал в акции автомобильного концерна А и строительного предприятия В. Чтобы уменьшить риск, акций А должно быть приобретено по крайней мере в два раза больше, чем акций В, причем последних можно купить не более чем на 100 тыс. ден. ед.
Дивиденды по акциям А составляют 8% в год, по акциям В – 10%. Какую максимальную прибыль можно получить в первый год?
Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на минимум и почему?
Сижу с этой задачей уже неделю.